| n | Assignments |
|---|---|
| 10 | 252 |
| 20 | 184,756 |
| 30 | 1.55 × 108 |
| 40 | 1.38 × 1011 |
| 50 | 1.26 × 1014 |
| 100 | 1.01 × 1029 |
| 200 | 9.05 × 1058 |
| 300 | 9.38 × 1088 |
4 Simple Randomized Experiments
\[ \DeclareMathOperator{\E}{\mathbb{E}} \DeclareMathOperator{\R}{\mathbb{R}} \DeclareMathOperator{\var}{Var} \DeclareMathOperator{\cov}{Cov} \newcommand{\ind}{\mathbb{I}} \newcommand{\onevec}{\mathbf{1}} \newcommand{\T}{^\mathsf{T}} \]
Let’s begin by considering a simple experiment.
Example 4.1 (Binomial experiment) We have \(n\) experimental units, indexed \(i = 1, \dots, n\). There is one treatment factor with two levels. Denote the treatments as \(Z_i \in \{0, 1\}\).
Each unit has potential outcomes \(C_i(0)\) and \(C_i(1)\). We observe the response \(Y_i = C_i(Z_i)\).
The first thing for us to consider is: What are the random variables, what is fixed, and what quantity do we want to estimate?
There are many ways to answer these questions, and surprisingly, there are even several ways to decide what is random and what is fixed.1 We’ll start with a conceptually simple one that works well when we consider causal questions; later we will switch.
4.1 Finite-population design
For now, then, we will assume that the \(n\) experimental units are our population. They are not sampled from anything—they are the entire population of interest. Because there is no random sampling, the potential outcomes \(C_i(0)\) and \(C_i(1)\) are fixed, not random. However, we may decide to assign \(Z_i\) randomly, and so \(Y_i\) can be random.
If we assign \(Z_i\) randomly, then all the random variation in \(Y_i\) is within our control—it is the result of our random assignment. In this setup, there is no “noise”; there is no \(\epsilon_i\) term that is normally distributed, or anything of the sort. There is just the fixed tuple \((C_i(0), C_i(1))\) for every experimental unit.
We then must define our estimand, i.e., the population quantity we want to estimate. A reasonable one is the average treatment effect.
Definition 4.1 (Average treatment effect) The average treatment effect (ATE) \(\bar \tau\) is the average causal effect of treatment across all experimental units: \[\begin{align*} \bar \tau &= \frac{1}{n} \sum_{i=1}^n (C_i(1) - C_i(0))\\ &= \frac{1}{n} \sum_{i=1}^n C_i(1) - \frac{1}{n} \sum_{i=1}^n C_i(0). \end{align*}\]
In this setting, the ATE is fixed, not random. It is a feature of our population of \(n\) experimental units, and we’d like to estimate it. We can’t simply plug numbers into the formula, however, because we only observe \(Y_i\)—we only observe one potential outcome for each unit, not both.
Hence we need an estimator. It would seem obvious to use the counterfactuals we do know: use \(Y_i\) when \(Z_i = 0\) for \(C_i(0)\), and use \(Y_i\) when \(Z_i = 1\) for \(C_i(1)\). We arrive at the mean difference estimator.
Definition 4.2 (Mean difference estimator for the ATE) The mean difference estimator for the average treatment effect, when the treatment \(Z_i\) is binary, is \[ \hat \tau = \frac{1}{n_1} \sum_{i : Z_i = 1} Y_i - \frac{1}{n_0} \sum_{i: Z_i = 0} Y_i, \] where \(n_1\) and \(n_0\) are the number of observations receiving treatments 1 and 0, respectively. We can also write this estimator in terms of \(C\) and \(Z\) directly: \[ \hat \tau = \frac{1}{n} \sum_{i=1}^n \left( \frac{Z_i C_i(1)}{n_1 / n} - \frac{(1 - Z_i) C_i(0)}{n_0 / n}\right). \] This is valid because \(Z_i\) is only 0 or 1, and we have constructed it so we only use counterfactual values that are observed.
Next, as with any statistical estimator, we can ask: Is this a good estimator? Or, more specifically, what are its bias and variance? To answer this, we must determine the distribution of \(Z_i\). We can start by ruling certain distributions right out.
Example 4.2 (A bad treatment assignment strategy) Suppose \(\bar \tau = 0\), but there is variation from unit to unit. Every unit has the same \(C_i(0)\), but for half the units, \(C_i(1) > C_i(0)\); in the other half, \(C_i(1) < C_i(0)\). The amounts average out to zero average treatment effect.
Suppose we choose \[ Z_i = \begin{cases} 1 & \text{if $C_i(1) > C_i(0)$}\\ 0 & \text{otherwise.} \end{cases} \] Then all cases with \(Z_i = 1\) will have larger response values than all cases with \(Z_i = 0\), and \(\hat \tau > 0\), despite \(\bar \tau = 0\). The estimator will be biased.
Exercise 4.1 (Realistic bad treatment assignments) Example 4.2 seems unrealistic because it requires us to know all the counterfactuals to assign treatments. But approximate versions of it can happen.
Consider an experiment on two treatments for a disease. We enroll \(n\) patients with the disease. A nurse examines the patients and then assigns them to treatment 0 or 1. Concoct a plausible scenario where something like Example 4.2 could happen.
This example demonstrates the same lesson we learned when discussing causality in Chapter 2: To estimate the causal effect of \(Z\) on \(Y\), \(Z\) must be made independent of any confounding variables that are associated with \(Y\) (or equal to it, in this case).
4.2 The Bernoulli experiment
The simplest experimental design is the Bernoulli experiment, which randomly assigns treatments independently.
Definition 4.3 (Bernoulli experiment) In an experiment with a binary treatment factor \(Z_i \in \{0, 1\}\), a Bernoulli design draws treatments independently from \[ Z_i \sim \operatorname{Bernoulli}(p). \] Usually \(p = 1/2\).
Yes, \(Z_i\) is random (and very easy to work with), but \(n_0\) and \(n_1\) are also random: in repeated experiments, we may assign different numbers of units to each treatment. In the worse case, with probability \((1/2)^n\) we might assign everyone to treatment 1 and have no data on treatment 0, which seems undesirable.
Exercise 4.2 (Allocation in a Bernoulli experiment) Let \(N_1\) be the random variable counting the number of units assigned to treatment \(Z_1 = 1\) in a Bernoulli experiment with treatment probability \(p\). What is the distribution of \(N_1\)?
It may be wiser to choose \(n_0\) and \(n_1\) in advance, both to eliminate this problem and, as we will see, give us more control over the variance of our estimates. So let’s try that.
4.3 Completely randomized experiments
The next experimental design is the completely randomized experiment, in which we choose the number of units to receive each treatment, then randomly assign.
Definition 4.4 (Completely randomized experiment) In an experiment with a binary treatment factor \(Z_i \in \{0, 1\}\), a completely randomized experiment fixes \(n_1\), the number of units to receive treatment \(Z_i = 1\). We draw \(n_1\) units uniformly at random, and without replacement, from the \(n\) units in the population, and assign these \(Z_i = 1\). All other units are assigned \(Z_i = 0\).
Finally we can reconsider our estimator \(\hat \tau\) from Definition 4.2, starting with its expectation.
Theorem 4.1 (ATE in the CRD) In a completely randomized experiment, the mean difference estimator \(\hat \tau\) (Definition 4.2) is unbiased.
Proof. To emphasize that the potential outcomes are fixed, not random, we will write the estimator as conditional on \(C(0)\) and \(C(1)\), the vectors of potential outcomes for all units. Because \(n_0\) and \(n_1\) are fixed, we do not need to include them in the expectations: \[\begin{multline*} \E[\hat \tau \mid C(0), C(1)] = \frac{1}{n} \sum_{i=1}^n \left( \frac{\E[Z_i C_i(1) \mid C(0), C(1)]}{n_1 / n} \right. \\ \left. - \frac{\E[(1 - Z_i) C_i(0) \mid C(0), C(1)]}{n_0/n} \right). \end{multline*}\] Here \(C_i(1)\) and \(C_i(0)\) are fixed, so they can come out of the expectation. And by design, \[\begin{align*} \E[Z_i \mid C(0), C(1)] &= \Pr(Z_i = 1 \mid C(0), C(1))\\ &= n_1 / n \\ \E[1 - Z_i \mid C(0), C(1)] &= \Pr(Z_i = 0 \mid C(0), C(1))\\ &= n_0 / n, \end{align*}\] because \(Z_i\) is drawn independently of \(C(0)\) and \(C(1)\). Hence the expectation simplifies to \[ \E[\hat \tau \mid C(0), C(1)] = \frac{1}{n} \sum_{i=1}^n (C_i(1) - C_i(0)) = \bar \tau, \] proving the estimator is unbiased.
We should not understate what we have proven here: By appropriately randomizing our experiment, we can use just the observed data (\(Y\)) to estimate a causal effect that is defined in terms of unobserved data (the counterfactuals \(C_i\)). This is true regardless of the presence of other variables associated with the counterfactuals! Without the random assignment, there could be confounding variables that account for any association between \(Z_i\) and \(Y_i\), but under random assignment such confounding is not possible.
As a statistician, you have learned many situations where correlation does not prove causation—but we have just shown that in an appropriately designed experiment, correlation can estimate causation.
4.4 Testing sharp nulls
It is a truth universally acknowledged, that a statistician in possession of data, must be in want of a hypothesis test.
Now, a hypothesis test may not be the best answer to the research question (and it often is not!), but they are popular nonetheless. Constructing a hypothesis test here will also help us better understand the problem setting and our assumptions.
We must first consider which null hypothesis to test. There are two obvious ones we can define:
Definition 4.5 (Sharp null) The sharp null hypothesis is \[ H_0: C_i(0) = C_i(1), \] for all \(i \in \{1, \dots, n\}\). In short, there is no treatment effect for any experimental unit.
Definition 4.6 (Average treatment effect null) The average treatment effect null hypothesis is \[ H_0: \bar \tau = 0, \] where \(\bar \tau\) is defined as in Definition 4.1. In short, there may be treatment effects for particular experimental units—we could have \(C_i(0) \neq C_i(1)\) for some \(i\)—but the effects average to zero.
4.4.1 The test procedure
You can certainly imagine both null hypotheses being useful in particular situations. But the sharp null is particularly appealing for defining tests—because when the sharp null hypothesis is true, we know all the counterfactuals. We only observe \(Y_i = C_i(Z_i)\), but when \(H_0\) is true, \(C_i(0) = C_i(1) = Y_i\).
We can use this fact to define a simple test of the sharp null hypothesis.
Definition 4.7 (Randomization test for the sharp null) We conduct an experiment by randomly assigning \(Z = (Z_1, Z_2, \dots, Z_n)\) and observing \(Y\). To test the sharp null hypothesis, we calculate the distribution of a test statistic under the null hypothesis:
- Calculate a test statistic \(T\) on the original data.
- Draw a new treatment assignment vector \(Z^*\) using the same procedure you used to draw the original treatment assignment.
- Calculate your test statistic using \(Z^*\) and \(Y\). Because \(C_i(0) = C_i(1)\) when the null is true, you can reuse \(Y_i\) even if \(Z_i^* \neq Z_i\). Call the new test statistic \(T^*\).
- Repeat steps 1 and 2 for every possible treatment assignment vector \(Z^*\).
A common test statistic is the absolute value of the mean difference (Definition 4.2), \(T = | \hat \tau |\). Using the absolute value makes the test sensitive to positive or negative treatment effects.
To calculate the \(p\)-value of the test, compare the original test statistic to the distribution you obtain under the null hypothesis: \[ p = \frac{1}{{n \choose n_0}} \sum \ind(T^*_i \geq T). \]
Example 4.3 (Randomization test for the sharp null) Consider a simple binomial experiment where \(n = 6\). There are two treatments and we use a completely randomized design with \(n_0 = n_1 = 3\). Suppose the true counterfactuals and results of the experiment are:
| Unit | \(C_i(0)\) | \(C_i(1)\) | \(Z_i\) | \(Y_i\) |
|---|---|---|---|---|
| 1 | 3 | 4 | 1 | 4 |
| 2 | 2.7 | 3.2 | 0 | 2.7 |
| 3 | 3.5 | 3.6 | 0 | 3.5 |
| 4 | 3.7 | 3.5 | 1 | 3.5 |
| 5 | 2.9 | 4.2 | 1 | 4.2 |
| 6 | 2.8 | 3.9 | 0 | 2.8 |
Of course, we only observe \(Z_i\) and \(Y_i\), and not both counterfactuals. But hypothetically, the true average treatment effect is \[ \bar \tau = \frac{1}{6} (4 + 3.2 + 3.6 + 3.5 + 4.2 + 3.9) - \frac{1}{6} (3 + 2.7 + 3.5 + 3.7 + 2.9 + 2.8) = 0.63, \] while the estimate from the observed data is \[ \hat \tau = \frac{1}{3} (4 + 3.5 + 4.2) - \frac{1}{3} (2.7 + 3.5 + 2.9) = 0.9. \]
To test the sharp null, we consider all possible treatment assignment vectors. Because we used completely randomized assignment, every possible treatment assignment vector has \(n_0 = n_1 = 3\). There are hence \({6 \choose 3} = 20\) possible vectors, including the one we actually used in the experiment.
For example, one possible new vector \(Z^*\) is
| Unit | \(Z_i^*\) | \(Y_i\) |
|---|---|---|
| 1 | 1 | 4 |
| 2 | 1 | 2.7 |
| 3 | 1 | 3.5 |
| 4 | 0 | 3.5 |
| 5 | 0 | 4.2 |
| 6 | 0 | 2.8 |
Again, under the null hypothesis the observed \(Y_i\) is the same as in the true experiment, because \(C_i(0) = C_i(1)\) under the null. We can recalculate the test statistic, obtaining \[ \hat \tau^* = -0.1, \] and repeat this procedure for all 18 other possible vectors. The \(p\) value is then the fraction of \(\hat \tau^*\) values equal to or more extreme than the observed \(\hat \tau\).
This test is exact and easy to define, but it has a price: the number of possible treatment assignments grows rapidly with \(n\). Consider completely randomized experiments with one binary treatment, assigning half of experimental units to each treatment. Table 4.1 shows how many possible treatment assignments are possible for different sample sizes.
Obviously the full randomization test becomes impractical for even modest values of \(n\), and essentially impossible for \(n\) larger than about 50 or so. We can, however, approximate the test statistic: Draw 1,000 (or 10,000, or whatever number is feasible) treatment assignment vectors uniformly at random from the set of possible treatment assignment vectors, rather than enumerating all possibilities.
Exercise 4.3 (Obtaining confidence intervals) Consider alternative hypotheses of the form \[ H_A: C_i(1) = C_i(0) + \delta. \] Here \(\delta\) is an effect size, and \(\delta = 0\) corresponds to the sharp null \(H_0\).
Describe how to use the randomization test (Definition 4.7) to obtain a 95% confidence interval for \(\delta\).
4.4.2 Test statistics
In Example 4.3, we used the estimated average treatment effect as the test statistic. But part of the appeal of the randomization test is that it is easily applied to any reasonable test statistic: the test does not rely on the mathematical derivation of distribution properties of any particular test statistic, so as long as we can compute the test statistic, we can compute the \(p\) value.
Different test statistics will have different properties, including different power against various alternative hypotheses. The considerations here are similar to any test comparing the distributions of two samples. Using the difference in means, as we have done, provides a test well-suited for alternative hypotheses where \(C_i(0)\) and \(C_i(1)\) have similar distributions but with different means, such as the alternative \[ H_A: C_i(1) = C_i(0) + \delta. \]
However, suppose the alternative hypothesis is instead multiplicative, e.g., \[ H_A: C_i(1) = \delta C_i(0), \] for some \(\delta \neq 1\). A better test statistic might be to log-transform \(Y\) first, then estimate the average treatment effect. On the log scale, this becomes an additive difference, and the mean difference is well-suited to detect it.
The mean difference can also run into problems when the true distributions of \(C_i(0)\) and \(C_i(1)\) have outliers, significant skew, or long tails. Another option is to use the ranks of \(Y\) instead of its values. This transforms the observed \(Y\) to integer values from 1 to \(n\), making them completely insensitive to the particular shape of the distribution or any outliers.
TODO simulations like Imbens and Rubin (2015) section 5.6, but with the right Y axis labels
4.5 Estimating the variance
While the sharp null hypothesis is (relatively) easy to test, it may not seem particularly realistic in practice. In an experiment testing a new drug to treat a disease, do we really believe it could have exactly zero effect for every patient? To decide whether it should be recommended for general use, we’re more likely to care about the average treatment effect: does the drug, on average, benefit patients? It may benefit some patients more than others, but as long as it is an average benefit, it can be approved for use.
However, the average treatment effect null (Definition 4.6) is not amenable to the randomization test procedure, because it does not permit us to fill in the unobserved values of \(C_i(0)\) and \(C_i(1)\). We will need some other test procedure and some other way to make confidence intervals. Let’s try to use the standard statistical procedure for making tests:
- Define a test statistic, such as the mean difference estimator for the ATE (Definition 4.2).
- Obtain an approximate distribution for that test statistic under the null hypothesis.
- Estimate the parameters (such as the variance) of that null distribution.
- Compare the observed test statistic to the approximate distribution under the null to get a \(p\) value.
We might guess that a reasonable approximate null distribution might be the normal distribution, since (a) statisticians always use the normal distribution and (b) the Central Limit Theorem provides that means are approximately normally distributed under the right circumstances. However, this requires extra justification: the CLT is usually applied to random variables that are random samples from some population, but here the population is finite and \(Y_i\) is only random because the treatment assignment \(Z_i\) is random. Nonetheless, we can apply a finite population CLT to justify approximate normality (Rosén 1964, theorem 12.1).
To use the normal distribution to construct tests and confidence intervals, we must know its mean and variance under the null. The mean is easy: under the null hypothesis, its mean should be zero. Let’s consider its variance.
4.5.1 Sampling variance with two experimental units
Calculating the variance of the mean difference estimator is not trivial: the randomness comes from our assignment of \(Z_i\), so the distribution is discrete (corresponding to the discrete values of \(Z_i\)). To simplify the problem, let’s consider a completely randomized design with \(n_0 = n_1 = 1\) (and hence \(n = 2\)), following Imbens and Rubin (2015), section 6.4.1.
The population ATE (Definition 4.1) is \[ \bar \tau = \frac{1}{2} \left( (C_1(1) - C_1(0)) + (C_2(1) - C_2(0)) \right). \] Because one unit must receive treatment 1 and the other must receive treatment 0, \(Z_1 = 1 - Z_2\), our estimator (Definition 4.2) is \[\begin{align*} \hat \tau &= \begin{cases} Y_2 - Y_1 & \text{if $Z_1 = 0$, $Z_2 = 1$}\\ Y_1 - Y_2 & \text{if $Z_1 = 1$, $Z_2 = 0$} \end{cases}\\ &= Z_1 (Y_1 - Y_2) + (1 - Z_1) (Y_2 - Y_1)\\ &= Z_1 (C_1(1) - C_2(0)) + (1 - Z_1) (C_2(1) - C_1(0)). \end{align*}\] Now, let \(D = 2 Z_1 - 1\), so that \(D \in \{-1, 1\}\), and \[\begin{align*} Z_1 &= \frac{1 + D}{2}, & Z_2 &= \frac{1 - D}{2}. \end{align*}\] By expanding this out and rearranging terms, we can write \[\begin{align*} \hat \tau &= \frac{1 + D}{2} (C_1(1) - C_2(0)) + \frac{1 - D}{2}(C_2(1) - C_1(0))\\ &= \frac{1}{2} [(C_1(1) - C_2(0)) + (C_2(1) - C_1(0))] + \frac{D}{2} [(C_1(1) - C_2(0)) - (C_2(1) - C_1(0))] \\ &= \bar \tau + \frac{D}{2} [(C_1(1) + C_1(0)) - (C_2(1) + C_2(0))]. \end{align*}\] Now, we have \[ \E[D \mid C(0), C(1)] = 2 \E[Z_1 \mid C(0), C(1)] - 1 = 2 \frac{1}{2} - 1 = 0, \] so we have verified that \(\hat \tau\) is unbiased for \(\bar \tau\). But we knew that already. We can, however, use this to get the variance, as the only random quantity is \(D\). We know that \[ \var(D) = \E[D^2] - \E[D]^2 = \E[D^2] - 0 = 1, \] since \(D \in \{-1, 1\}\). We can hence calculate \[\begin{align*} \var(\hat \tau) &= \frac{\var(D)}{4} [(C_1(1) + C_1(0)) - (C_2(1) + C_2(0))]^2\\ &= \frac{1}{4} [(C_1(1) + C_1(0)) - (C_2(1) + C_2(0))]^2. \end{align*}\] So the sampling variance of \(\hat \tau\) depends on all of the counterfactuals, including the unobserved ones.
4.5.2 Sampling variance in general
Extending this to \(n > 2\) is nontrivial because it requires a great deal more algebra and complicated expectations, but it can be done:
Theorem 4.2 (Sampling variance of the mean difference estimator) In a completely randomized experiment with two treatment levels, conducted in a population of \(n\) experimental units, the variance of the mean difference estimator \(\hat \tau\) (Definition 4.2) is \[ \var(\hat \tau) = \frac{S_0^2}{n_0} + \frac{S_1^2}{n_1} - \frac{S_{01}^2}{n}, \] where \[\begin{align*} S_j^2 &= \frac{1}{n-1} \sum_{i=1}^n (C_i(j) - \bar C(j))^2\\ S_{01}^2 &= \frac{1}{n-1} \sum_{i=1}^n ((C_i(1) - C_i(0)) - \bar \tau)^2. \end{align*}\] The quantities \(\bar C(0)\) and \(\bar C(1)\) are the population averages of the counterfactuals, making the variance the sum of three components:
- The population variance of \(C_i(0)\)
- The population variance of \(C_i(1)\)
- The population variance of \(C_i(1) - C_i(0)\), the treatment effects for each unit.
Proof. See appendix A to chapter 6 of Imbens and Rubin (2015).
The meaning of each variance term is illustrated in Figure 4.1. The first two terms of the variance are intuitive: if we are estimating a difference in means, the variance depends on the variance of the quantities we are taking the means of. The third term is a little less intuitive, but suggests the sampling variance is the largest if every unit has the same treatment effect, and is smaller if every unit has a different treatment effect.
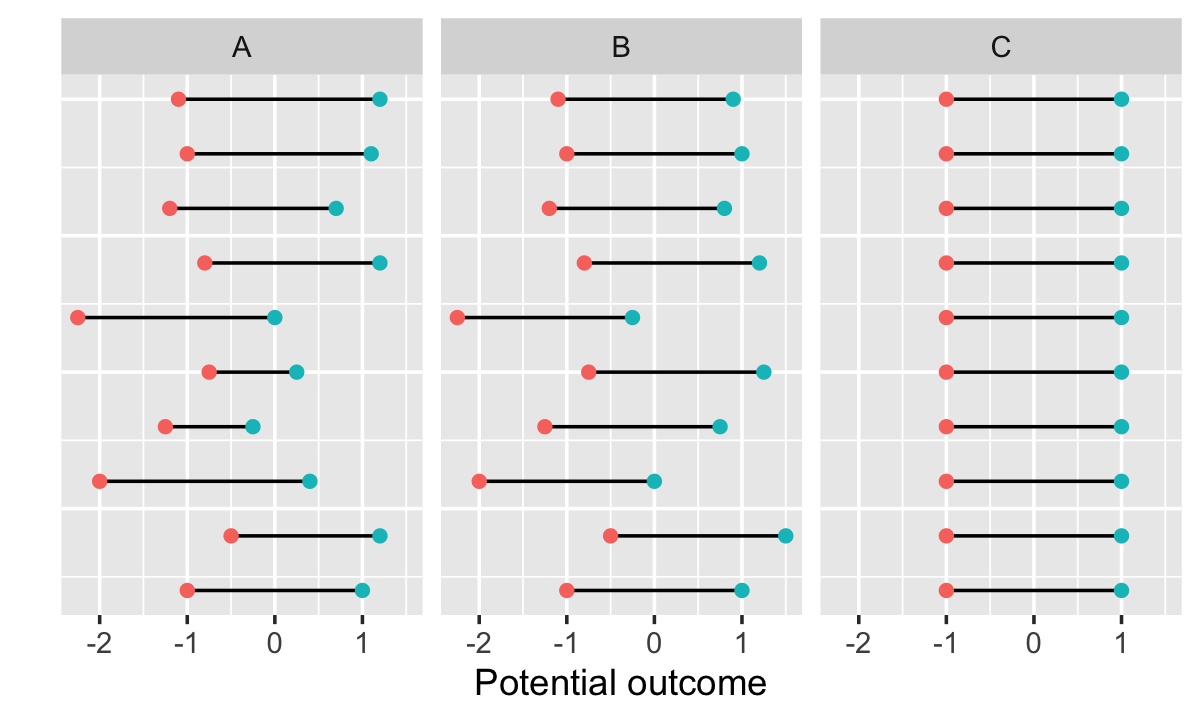
This is actually good for us: We can estimate the first two terms, but the third term depends upon the individual unit treatment effects, which we never observe—and hence cannot easily estimate. But if we assume all units have the same treatment effect, \(S_{01}^2 = 0\), and we get a variance estimate that is conservative: it is always larger than the variance when the treatment effects differ. We can safely use this and get conservative tests and confidence intervals.
This leads to the estimator.
Theorem 4.3 (Estimating the sampling variance) In a completely randomized experiment with two treatment levels, conducted in a population of \(n\) experimental units, the variance given in Theorem 4.2 can be estimated by \[ \widehat{\var}(\hat \tau) = \frac{s_0^2}{n_0} + \frac{s_1^2}{n_1}, \] where \[ s_j^2 = \frac{1}{n_j - 1} \sum_{i : Z_i = j} \left(Y_i - \frac{1}{n_j} \sum_{k: Z_i = j} Y_k \right)^2, \] the sample variance of the observed values of the counterfactuals.
When the treatment effect \(C_i(1) - C_i(0)\) is constant for all \(i\), this estimator is unbiased.
We can also use the sampling variance to answer a natural question: for a fixed \(n\), what values of \(n_0\) and \(n_1\) should I choose to estimate \(\hat \tau\) with the least variance?
Exercise 4.4 (Choosing treatment allocations) Consider a completely randomized experiment with two treatment levels. We have \(n\) experimental units available. Suppose \(S_0^2 = S_1^2\), and conservatively assume \(S_{01}^2 = 0\). What values of \(n_0\) and \(n_1\) minimize \(\var(\hat \tau)\)?
4.6 Testing the average treatment effect
Armed with an estimator for the variance of \(\hat \tau\), we can produce confidence intervals and tests.
For confidence intervals, we may assume that \(\hat \tau\) is approximately normally distributed, as described above, and that \(\widehat{\var}(\hat \tau)\) is approximately \(\chi^2\), meaning \(\hat \tau / \sqrt{\widehat{\var}(\hat \tau)}\) is approximately \(t\)-distributed. However, we’d have to work out the right degrees of freedom, and that doesn’t sound fun, so let’s instead assume it’s approximately standard normal.
If so, we can construct the usual confidence intervals based on the quantiles of the normal distribution: \[ \left( \hat \tau + z_{\alpha/2} \sqrt{\widehat{\var}(\hat \tau)}, \hat \tau + z_{1 - \alpha/2} \sqrt{\widehat{\var}(\hat \tau)} \right). \] And we can use ordinary \(z\) tests to test nulls involving the ATE, such as Definition 4.6.
Unlike the randomization test for the sharp null and its associated confidence interval, these tests and CIs are approximate. They rely on a large-sample approximation to the distribution of \(\hat \tau\) rather than exactly obtaining the distribution.
Nonetheless, they resemble the confidence intervals and tests you’d expect to calculate in an introductory statistics course. But unlike the tests in an intro class, the only random variable is \(Z_i\), the treatment assignments—we are not assuming an infinite population from which our sample is drawn, and there is no error term \(\epsilon\) with a certain assumed distribution.
4.7 Exercises
Exercise 4.5 (Variance and covariance of treatment indicators) Consider a completely randomized experiment (Definition 4.4) with \(n\) experimental units. Of these, \(n_1\) units get the treatment (\(Z_i = 1\)) and \(n_0\) get the control (\(Z_i = 0\)).
- Calculate \(\E[Z_i]\), \(\E[Z_i^2]\), and \(\var(Z_i)\).
- What is \(\E[Z_i \mid Z_j = 1]\), for \(i \neq j\)?
- Calculate \(\cov(Z_i, Z_j)\) for \(i \neq j\).
- Use \(\var(Z_i)\) and \(\cov(Z_i, Z_j)\) to derive a matrix expression for \(\var(Z)\). Hint: It may be useful to use \(\onevec\), the vector of all ones, and \(\onevec \onevec\T\), a matrix of all ones.
Simplify each result as best as you can in terms of \(n_0\), \(n_1\), and \(n\). Comment on the final result: are \(Z_i\) and \(Z_j\) independent? Is this surprising?
Exercise 4.6 (Generating a completely randomized design) We will use R simulations throughout the course to illustrate experimental design concepts. We’ll need a way to generate completely randomized designs.
Write a function with the following signature:
#' @param levels Number of treatment levels
#' @param ns Vector of length `levels`, giving the number of units to be
#' assigned to each treatment level
#' @return Data frame with an `assignment` column, with one row per unit,
#' containing integers 1, ..., levels, representing the level to which each
#' unit is assigned.
completely_randomized <- function(levels, ns) {
# TODO fill in
}It should work like this:
> completely_randomized(2, c(3, 2)) assignment
1 1
2 2
3 1
4 1
5 2And, of course, it should be random, generating a new completely randomized design each time it is called. Show one example experiment output to demonstrate your function works correctly.
Exercise 4.7 (Simulating a completely randomized experiment) Continuing from Exercise 4.6, let’s build a function that can observe data from a particular completely randomized design. Suppose we are given a data frame with one row per unit and columns for the counterfactuals \(C_i(j)\) for every treatment level \(j\). These columns will all have names beginning with treatment, so treatment1 is \(C_i(1)\), treatment2 is \(C_i(2)\), and so on. There may be other columns of covariates as well. This data frame represents the true population and its true counterfactuals.
We then obtain an experimental design with completely_randomized(), ensuring sum(ns) matches the size of this population.
Write a function to select the observed responses corresponding to the treatments for each unit:
#' @param population Data frame representing the population, with columns
#' `treatment1`, `treatment2`, and so on representing the counterfactuals for
#' each unit.
#' @param design Experimental design from `completely_randomized()`. Must have
#' the same number of rows as `population`.
#' @return Data frame with the same rows and columns as `population`, plus two new
#' columns:
#' - `response`, containing the observed Y value for each unit
#' - `treatment`, containing the treatment level for each unit from the design.
observe <- function(population, design) {
# TODO fill in
}Exercise 4.8 (Testing a completely randomized experiment) Download sim-crd.csv and load it in R. This data frame contains the covariates and potential outcomes of 100 experimental units:
crd <- read.csv("data/sim-crd.csv")
head(crd) prior_grade year treatment1 treatment2
1 A junior 12.017082 9.365763
2 C junior 3.623687 4.558320
3 A junior 8.811771 10.844473
4 A junior 9.834920 7.593980
5 A junior 11.143657 10.058124
6 B sophomore 8.372420 7.992201Here the experimental units are students in a statistics course. The instructor plans to try two different ways of teaching them about interactions, then give them a short test about interactions. The treatment1 and treatment2 columns give the potential outcome of each student under each treatment. The prior_grade column records each student’s grade in the course so far, and year is their academic year. The instructor suspects these may also be associated with their scores on the test.
Of course, normally we would not know both potential outcomes, but this is a religious school and the data was received by divine intervention. Let’s use it to explore completely randomized designs and randomization tests.
Calculate the population average treatment effect \(\bar \tau\) (Definition 4.1). Is the treatment effect nonzero? If so, which treatment produces the highest test scores?
Also calculate the individual treatment effects, \(C_i(1) - C_i(0)\). Are these zero or nonzero? State whether the sharp null (Definition 4.5) and the average treatment effect null (Definition 4.6) are true or false in this dataset.
Now let’s suppose we’d like to run the experiment. Use your
completely_randomized()function from Exercise 4.6 to generate a treatment assignment that assigns half of the students to each treatment. Then use yourobserve()function from Exercise 4.7 to add aresponsecolumn giving the response (test score) for each student in this experiment. Calculate \(\hat \tau\), your estimate of the mean treatment effect in this experiment.Now conduct a randomization test for the sharp null. If you call
completely_randomized()repeatedly, you can replace the treatment assignments in the data frame without changing the observed response, allowing you to generate new data frames under the null. Use 1,000 replications rather than enumerating every possible treatment assignment. Use \(| \hat \tau |\) as your test statistic. Report a \(p\) value.Finally, let’s consider the power of this test. Each randomized experiment will produce a different estimate \(\hat \tau\); we happened to get one value in part 2, but would obtain a different value if we ran the experiment again. Some of these will be statistically significant and some will not. Run steps 2 and 3 100 times and report the fraction of tests that are significant. This is the power of this test to detect the deviations from the null present in this dataset.
And I’m not even counting the Bayesian way.↩︎