6 Linear Models for Experiments
\[ \DeclareMathOperator{\E}{\mathbb{E}} \DeclareMathOperator{\R}{\mathbb{R}} \DeclareMathOperator{\RSS}{RSS} \DeclareMathOperator{\var}{Var} \DeclareMathOperator{\cov}{Cov} \newcommand{\ind}{\mathbb{I}} \newcommand{\T}{^\mathsf{T}} \newcommand{\X}{\mathbf{X}} \newcommand{\Y}{\mathbf{Y}} \newcommand{\tsp}{\bar \tau_\text{sp}} \newcommand{\tsphat}{\hat \tau_\text{sp}} \DeclareMathOperator*{\argmin}{arg\,min} \]
In Chapter 4, we began with a conceptually very simple model: We have \(n\) fixed experimental units, their potential outcomes are well-defined, and their responses are random only because we performed random assignment. This gives us complete control over the randomness and permits exact randomization tests.
However, this approach will prove limiting, particularly when we want to experiment on multiple treatment factors simultaneously, while blocking and controlling for covariates. The estimators become harder to define and work with. Can we use an approach that more easily handles multiple factors and covariates? Sure, if we use a model. Let’s consider our favorite models: linear models.
6.1 Super-population design
In the finite-population design (Section 4.1), our \(n\) experimental units formed the entire population. This allowed us to define the population average treatment effect as a sum over all \(n\), and ensured the counterfactuals were fixed, not random.
But we could also say that there is some hypothetical population distribution \(P\), from which our \(n\) experimental units are randomly sampled. Now the counterfactuals \(C_i(0)\) and \(C_i(1)\) are random, because unit \(i\) was randomly sampled from the population. We call this the “super-population” from which our population of \(n\) units comes. (Don’t ask why we don’t just call it the “population” from which our “sample” of \(n\) units comes.)
The population average treatment effect is now an expectation, not a sum.
Definition 6.1 (Average treatment effect) In the super-population model, the average treatment effect \(\tsp\) is \[\begin{align*} \tsp &= \E[C_i(1) - C_i(0)] \\ &= \E[C_i(1)] - \E[C_i(0)], \end{align*}\] where the expectations average over the superpopulation.
To estimate the ATE, we will evidently have to estimate \(\E[C_i(1)]\) and \(\E[C_i(0)]\). Let’s expand those expectations: \[\begin{align*} \E[C_i(1)] &= \E[ \E[C_i(1) \mid X_i] ] & \text{law of iterated expectation}\\ &= \E[ \E[C_i(1) \mid X_i, Z_i = 1] ] & \text{when $Z_i$ is independent of $C_i$}\\ &= \E[ \E[Y_i \mid X_i, Z_i = 1] ] & \text{because $Y_i = C_i(Z_i)$}. \end{align*}\] So if we can model the conditional mean of \(Y\) given \(X\) and the treatment assignment, then average over all \(X\), we can estimate the ATE. It’s just regression! We fit models for \(\E[Y_i \mid X_i, Z_i]\) and then use them to get the ATE.
Let’s apply this to a simple randomized experiment.
Example 6.1 (Completely randomized experiment, superpopulation-style) Consider a completely randomized experiment with two treatment levels, \(Z_i \in \{0, 1\}\), and no covariates. We choose to model \[\begin{align*} \E[Y_i \mid Z_i] &= \begin{cases} \beta_0 & \text{if $Z_i = 0$} \\ \beta_0 + \beta_1 & \text{if $Z_i = 1$}. \end{cases}\\ &= \beta_0 + \beta_1 Z_i \end{align*}\] Consequently, the average treatment effect \(\tsp\) is \[ \tsp = \E[\E[Y_i \mid Z_i = 1]] - \E[\E[Y_i \mid Z_i = 0]] = (\beta_0 + \beta_1) - \beta_0 = \beta_1, \] where the outer expectations average over the covariates \(X\), but here do nothing because there are no covariates.
Traditionally, simple linear models like these are fit using ordinary least squares (OLS). The parameters \(\beta_0\) and \(\beta_1\) are obtained by minimization: \[ \hat \beta_0, \hat \beta_1 = \argmin_{\beta_0, \beta_1} \sum_{i=1}^n (Y_i - (\beta_0 + \beta_1 Z_i))^2. \] See any regression textbook for details on least squares and the derivation of analytical forms for the estimates; see my 707 notes for examples of running regression in R. We then plug in the estimates \(\hat \beta_0\) and \(\hat \beta_1\) to get our treatment effect estimates.
Exercise 6.1 (The OLS estimator) The OLS estimators are so widely used that I picked a textbook off my shelf, opened it to a random page, and found the analytical solutions: \[\begin{align*} \hat \beta_1 &= \frac{\sum_{i = 1}^n (Z_i - \bar Z) (Y_i - \bar Y)}{\sum_{i=1}^n (Z_i - \bar Z)^2} & \hat \beta_0 &= \bar Y - \hat \beta_1 \bar Z, \end{align*}\] where \(\bar Y\) and \(\bar Z\) are the sample means of the two quantities.
Show that the OLS estimate of the treatment effect \(\hat \tau_\text{OLS} = \hat \beta_1\) is identical to the mean difference estimate, Definition 4.2.
In other words, in a randomized experiment, \(\beta_1 \neq 0\) really does mean that increasing \(Z_i\) from 0 to 1 causes a change in the mean of \(Y\).
Linear models open up the possibility of covariates: other measured features of the units, apart from the treatment assignment \(Z_i\), that may be associated with the response.
Example 6.2 (Superpopulation CRD with covariates) Let’s assume we have the treatment assignment \(Z_i\) plus a vector \(X_i\) of \(p\) covariates. We model \[ \E[C_i(j)] = \E[\E[Y_i \mid X_i, Z_i = j]], \] where the outer expectation is over the distribution of \(X\).
With two treatments, then, we need two separate models: \[\begin{align*} \E[Y_i \mid X_i, Z_i = 0] &= \beta_0 + X_i\T \beta\\ \E[Y_i \mid X_i, Z_i = 1] &= \beta_0^* + X_i\T \beta^*. \end{align*}\] Here the two models have different slopes and intercepts. But this is equivalent to having an interaction between \(Z_i\) and each covariate in \(X_i\): \[ \E[Y_i \mid X_i, Z_i] = \beta_0 + \beta_1 Z_i + X_i\T (\beta + \beta' Z_i). \] Compared to the previous form, \(\beta_0^* = \beta_0 + \beta_1\) and \(\beta^* = \beta + \beta'\).
Hence we can build a linear model for a randomized experiment with covariates by including a treatment indicator, covariates, and the appropriate interaction. To estimate the average treatment effect, we must use our model estimates to average over \(X\).
Example 6.3 (Binary treatment, binary covariate) Consider conducting an experiment with binary treatment \(Z_i \in \{0, 1\}\) and a binary covariate \(X_i \in \{0, 1\}\). For instance, \(X_i\) could be a discrete variable we block on. We build a linear model with three covariates: \[ \E[Y_i \mid X_i, Z_i] = \beta_0 + \beta_1 Z_i + \beta_2 X_i + \beta_3 X_i Z_i. \] Consider a grid where each column is a treatment, each row is a covariate value, and the entries are the conditional means:
| \(Z_i = 0\) | \(Z_i = 1\) | |
|---|---|---|
| \(X_i = 0\) | \(\beta_0\) | \(\beta_0 + \beta_1\) |
| \(X_i = 1\) | \(\beta_0 + \beta_2\) | \(\beta_0 + \beta_1 + \beta_2 + \beta_3\) |
How do we calculate the average treatment effect from Definition 6.1? Following Example 6.1, we find that \[\begin{align*} \tsp ={}& \E[\E[Y_i \mid X_i, Z_i = 1] - \E[Y_i \mid X_i, Z_i = 0]]\\ ={}& (\E[Y_i \mid X_i = 1, Z_i = 1] - \E[Y_i \mid X_i = 1, Z_i = 0]) \Pr(X_i = 1)\\ &{}+ (\E[Y_i \mid X_i = 0, Z_i = 1] - \E[Y_i \mid X_i = 0, Z_i = 0]) \Pr(X_i = 0), \end{align*}\] by the law of total expectation. In other words, the treatment effects conditional on \(X_i\) are the difference between the entries in the rows of the table. We can substitute in the values from our table to find that \[ \tsp = (\beta_1 + \beta_3) \Pr(X_i = 1) + \beta_1 \Pr(X_i = 0). \] We are, in effect, averaging the treatment effect from each row, proportional to how common those covariate values are in the population.
In practice, we would estimate \(\hat \beta_0\) through \(\hat \beta_3\) using OLS, and estimate \(\Pr(X_i)\) using the proportion in each group in our sample.
Exercise 6.2 (OLS estimate in blocked designs) Suppose that the covariate in Example 6.3 is a blocking variable. We can estimate the ATE using either the OLS approach shown or the blocked mean difference estimator, Definition 5.3. Show these are equivalent.
6.2 Variances in linear models
So far it appears that using ordinary least squares and the super-population approach yields identical point estimates to using treatment effect estimators in the finite population model. Before we decide to use least squares for everything,1 we should consider whether it also leads to the same inferences.
You’re probably familiar with the classic results for variance in OLS models. If we let \(\Y\) be the vector of \(n\) responses and \(\X\) be the full design matrix, and model \(\E[Y \mid X] = X \beta\) (where we’ve now added the intercept into \(X\)), the standard result is that \[ \var(\hat \beta \mid \X) = \sigma^2 (\X\T \X)^{-1}, \] where \(\sigma^2\) is the variance of the error: \(Y = X \beta + \epsilon\), and \(\sigma^2 = \var(\epsilon)\). This result assumes that \(\var(\epsilon)\) is uncorrelated with \(X\); the more general result is that \[ \var(\hat \beta \mid \X) = (\X\T \X)^{-1} \X\T \var(\Y \mid \X) \X (\X\T \X)^{-1}. \] This leads us to the sandwich estimator for the variance.
Definition 6.2 (Sandwich estimator) The sandwich estimator, also known as the Huber–White estimator, for the variance of \(\hat \beta\) in an ordinary least squares regression is \[ \widehat{\var}(\hat \beta \mid \X) = (\X\T \X)^{-1} \X\T \widehat{\var}(\Y \mid \X) \X (\X\T \X)^{-1}, \] where we estimate \(\widehat{\var}(\Y \mid \X)\) as a diagonal matrix with potentially unequal entries: \[ \widehat{\var}(\Y \mid \X) = \begin{pmatrix} \hat \epsilon_1^2 & 0 & \cdots & 0 \\ 0 & \hat \epsilon_2^2 & 0 & \vdots \\ \vdots & \vdots & \vdots & \vdots\\ 0 & \cdots & 0 & \hat \epsilon_n^2 \end{pmatrix} \] Here \(\hat \epsilon_i = Y_i - \hat \beta\T X_i\), and these are variance estimates because \(\var(\Y \mid \X) = \var(\X\beta + \epsilon \mid \X) = \var(\epsilon \mid \X)\), and \(\var(\epsilon) = \E[\epsilon^2] - \E[\epsilon]^2\), where the second term is assumed to be zero.
This estimator is valid even when the error variances are unequal, unlike the usual estimator.
(See the 707 notes for more details on sandwich estimators, including other variations of the estimator and calculating them in R.)
We can show that when we use the sandwich estimator, the variance we obtain matches the conservative variance estimate we developed for randomized experiments in the finite population setting.
Exercise 6.3 (Variance in a binary experiment) Consider an experiment with two treatments, \(Z_i \in \{0, 1\}\), and no covariates. We use the OLS model shown in Example 6.1 and the estimators in Exercise 6.1. Show that \[ \widehat{\var}(\hat \beta_1 \mid \X) = \frac{\sum_{i = 1}^n \hat \epsilon_i^2 (Z_i - \bar Z)^2}{\left( \sum_{i=1}^n (Z_i - \bar Z)^2 \right)^2} = \frac{s_1^2}{n_1} + \frac{s_0^2}{n_0}, \] where \(s_0^2\) and \(s_1^2\) are defined as in Theorem 4.3.
Because \(\tsphat = \hat \beta_1\), this says that \(\widehat{\var}(\tsphat \mid \X)\) matches the variance we previously obtained in the finite population case.
In short, we’ve found several important results here:
- In simple binary experiments, OLS gives exactly the same estimators as we already used in completely randomized experiments.
- The usual OLS variance estimates, derived from the assumption that \(Y\) is a random variable drawn from a population, match the conservative variance estimates we derived for finite-population completely randomized experiments.
- When we include covariates, such as blocking variables, the OLS estimates also match the finite-population estimates.
So regardless of whether we believe in finite populations or superpopulations, we can justify using ordinary least squares and linear models.
6.3 The general linear model framework
The finite-population and superpopulation ideas grew up around the same time in the 1930s, but by the 1950s, the superpopulation concept with linear models was the dominant form of experimental design. I’m no historian of statistics, but one obvious reason is the great flexibility of linear models to accommodate all kinds of wacky designs, and the ease of deriving variances and tests using asymptotic results and creative linear algebra.
Linear models for experimental design are traditionally written a little differently than you may be used to in regression. Consider an experiment with \(v\) treatments (which may be more than two). We might choose to model \[ Y_{it} = \mu + \tau_i + \epsilon_{it}, \] where \(i \in \{1, \dots, v\}\) is the treatment and \(t \in \{1, \dots, r_i\}\) is the experimental unit, and \(r_i\) is the number of units—the number of replications—in treatment \(i\). The errors \(\epsilon_{it}\) are assumed to be mean 0 and uncorrelated. Though above we allowed the errors to have unequal variance, it is common to assume that \(\var(\epsilon_{it}) = \sigma^2\), so all have equal variance. Together, the model implies that \[ \E[Y_{it}] = \mu + \tau_i. \]
You may already notice a problem with this model: it is not identifiable.
Definition 6.3 (Identifiability) Suppose a model is written as a function of some parameters: \(\E[Y] = f(\beta)\), where \(\beta\) is a vector of one or more parameters and \(f\) is an arbitrary function. The parameters are identifiable if for any \(\beta_1\) and \(\beta_2\), \(f(\beta_1) = f(\beta_2)\) implies \(\beta_1 = \beta_2\).
Or, in words: If the parameters are identifiable, then given a specific model, there is only one unique set of parameters that produces that model.
Exercise 6.4 (Non-identifiable model) The model \[ \E[Y_{it}] = \mu + \tau_i \] is not identifiable. Demonstrate this by giving an example of two sets of parameters that yield an identical model.
On the other hand, despite the model not being identifiable, the quantities we care about are estimable.
Definition 6.4 (Estimability) A function of the parameters of a linear model is estimable if it can be written as the expectation of a linear combination of the response variables.
For example, in the model above, \(\mu + \tau_i\) is estimable for any \(i\): simply take the expectation of any particular response with that \(i\). Indeed, all the quantities we need are estimable in the above model, even though it is not identifiable.
Exercise 6.5 (Estimability of the ATE) Consider a binary experiment. We model \[ Y_{it} = \mu + \tau_i + \epsilon_{it}, \] where \(i \in \{0, 1\}\) and \(t \in \{1, \dots, r_i\}\). What is the average treatment effect? Write it as an expectation, and then write it in terms of \(\mu\) and \(\tau\).
Nonetheless, software to do least squares estimates usually forces the model to be identifiable by imposing additional constraints. There are several common options:
- Require that \(\hat \mu = 0\). This makes the model identifiable and gives \(\tau_i\) easy interpretation.
- Force \(\hat \tau_1 = 0\) (or some other specific \(\tau\)). This matches R’s behavior: if treatment were coded as a binary factor, R fits an intercept (\(\mu\)) and a coefficient for one treatment level, but sets the other to zero.
- Require \(\sum_{i} r_i \hat \tau_i = 0\). TODO who does this?
With these constraints enforced, there is a unique least squares solution to estimate the parameters of the model. We can also think of these constraints as different ways to translate the model into the form \(\E[Y \mid X] = X \beta\), by constructing the right matrix \(\X\) so components of \(\beta\) correspond to our parameters of interest.
The model can easily be extended to handle blocking and even multiple treatment factors. For example, we could model \[ Y_{ijt} = \mu + \tau_{ij} + \epsilon_{ijt}, \] where \(i \in \{1, \dots, v\}\) is one treatment level, \(j \in \{1, \dots, u\}\) is the treatment level for the other treatment factor, and \(t \in \{1, \dots, r_{ij}\}\) indexes the experimental units in that treatment combination. We’ll consider more complex multi-factor experiments in Chapter 7.
In any of these models, we will need a way to estimate \(\var(\epsilon) = \sigma^2\). That poses a problem. Suppose \(r_{ij} = 1\) for all \(i\) and \(j\). There is only one replicate for each block and treatment—only one experimental unit in each combination. In that case, the model is no longer identifiable! The errors \(\epsilon_{ijt}\) are not uniquely determined, and so there is no variance. We must have more than one replicate in at least one treatment combination to estimate the variance, or we must simplify the model somehow. We’ll discuss options for multiple treatment factors further in Section 7.2.
To estimate the variance, we can adapt the usual result from linear regression. An unbiased estimator is \[ \hat \sigma^2 = \frac{\RSS}{n - p} = \frac{\sum_{i=1}^v \sum_{j=1}^u \sum_{t=1}^{r_{ij}} \left(Y_{ijt} - (\hat \mu + \hat \tau_{ij})\right)^2}{n - (v + u)}. \] This is the usual residual sum of squares, rewritten for our form of model, replacing \(p\) with the number of unique parameters estimated in our model.
6.4 Contrasts
In linear models, the coefficients are not always the answer to your research question. By this I mean that the individual parameters \(\mu\) or \(\tau_i\) do not themselves answer your research question, which instead is often answered by a linear combination of the parameters. For example, in Exercise 6.5, we found that the average treatment effect is a linear combination of the parameters.
We will find we often need linear combinations of parameters, and so they are given a name: contrasts.
6.4.1 Definition and estimation
Definition 6.5 (Contrasts) In a linear model defined as in Section 6.3, a contrast is a linear combination of parameters \(\tau\) defined by a vector of coefficients \(c\): \[ \sum_{i=1}^v c_i \tau_i, \qquad \text{where } \sum_{i=1}^v c_i = 0. \] The coefficient vector \(c = (c_1, \dots, c_v)\T\) is called the contrast vector.
All contrasts are estimable using ordinary least squares. As you might expect, when there is one treatment factor and no blocking, the least squares estimator is \[ \sum_{i=1}^v c_i \left( \frac{1}{r_i} \sum_{t=1}^{r_i} Y_{it} \right) = \sum_{i=1}^v c_i \hat \tau_i. \]
With the language of linear models and contrasts, it is easy to move beyond binary treatments to experiments with arbitrarily many treatment arms.
Exercise 6.6 (Treatment contrasts) Consider conducting an experiment where there are 4 treatment arms (so \(i \in \{1, 2, 3, 4\}\)). Write contrast vectors that estimate:
- The average treatment effect for the difference between treatment 3 and treatment 1
- The difference between the average response for treatment 1 and the average response for treatments 2, 3, and 4, weighted equally
- The difference between the average response of treatments 1 and 2 and the average response of treatments 3 and 4.
6.4.2 Inference
Contrasts can be used for inference.
Theorem 6.1 (Variance of contrasts) Because they are simple linear combinations, in a one-factor experiment we can calculate the variance of an estimated contrast as \[\begin{align*} \var\left( \sum_{i=1}^v c_i \hat \tau_i \right) &= \sum_{i=1}^v c_i^2 \var(\hat \tau_i)\\ &= \sum_{i=1}^v \frac{c_i^2}{r_i} \var(Y) \\ &= \sigma^2 \sum_{i=1}^v \frac{c_i^2}{r_i}. \end{align*}\]
As a linear combination of means, standard linear model theory and sampling theory justifies treating these estimates as approximately normal; when the errors are exactly normal, they are exactly normal. We can consequently estimate this variance and use it to conduct \(t\) tests for contrasts.
Theorem 6.2 (t test for a contrast) Let \(T = \sum_i c_i \tau_i\) be a contrast in an experiment with \(v\) treatments and \(r_i\) replicates per treatment. Let \(\hat T\) be its estimate and let \(n = \sum_i r_i\). Then, under the null hypothesis that \(T = t_0\), \[ \frac{\hat T - t_0}{\sqrt{\widehat{\var}(\hat T)}} \sim t_{n - v}, \] where the variance is estimated by plugging \(\hat \sigma^2\) into Theorem 6.1.
This result permits \(t\) tests for particular null hypotheses, such as the common null that \(T = 0\). We can also obtain confidence intervals from it.
Theorem 6.3 (Contrast confidence interval) We can obtain a \(1 - \alpha\) confidence interval for a contrast \(T = \sum_i c_i \tau_i\) as \[ \left[ \hat T - t_{n - v, 1- \alpha/2} \sqrt{\widehat{\var}(\hat T)}, \hat T - t_{n - v, \alpha/2} \sqrt{\widehat{\var}(\hat T)} \right]. \]
Proof. This follows from Theorem 6.2, which implies that \[\begin{align*} 1 - \alpha &= \Pr\left(t_{n - v, \alpha/2} \leq \frac{\hat T - T}{\sqrt{\widehat{\var}(\hat T)}} \leq t_{n - v, 1 - \alpha/2}\right)\\ &= \Pr\left( \hat T - t_{n - v, 1-\alpha/2} \sqrt{\widehat{\var}(\hat T)} \leq T \leq \hat T - t_{n - v, \alpha/2} \sqrt{\widehat{\var}(\hat T)}\right). \end{align*}\] This may look counterintuitive, but recall that \(t_{n-v, \alpha/2} < 0\) and \(t_{n-v, 1 - \alpha/2} = - t_{n - v, \alpha/2}\) because the \(t\) distribution is symmetric.
We may be interested in multiple contrasts, in which case their covariance will be of interest as well.
Theorem 6.4 (Covariance of contrasts) Consider two contrasts vectors \(c\) and \(c'\). The covariance of the estimated contrasts is \[ \cov\left( \sum_{i=1}^v c_i \hat \tau_i, \sum_{i=1}^v c_i' \hat \tau_i \right) = \sigma^2 \sum_{i=1}^v \frac{c_i c_i'}{r_i}. \]
Proof. Recall a basic property of covariances: \[\begin{multline*} \cov(aX + bY, cW + dZ) = ac \cov(X, W) + ad \cov(X, Z) \\ + bc \cov(Y, W) + bd \cov(Y, Z). \end{multline*}\]
In the contrast case, all the cross-terms are zero, as \(\cov(\hat \tau_i, \hat \tau_j) = 0\) for \(i \neq j\). (Why?)
We’re left with \[\begin{align*} \cov\left( \sum_{i=1}^v c_i \hat \tau_i, \sum_{i=1}^v c_i' \hat \tau_i \right) &= \sum_{i=1}^v c_i c_i' \cov(\hat \tau_i, \hat \tau_i)\\ &= \sum_{i=1}^v c_i c_i' \var(\hat \tau_i)\\ &= \sum_{i=1}^v c_i c_i' \frac{\var(Y)}{r_i}\\ &= \sigma^2 \sum_{i=1}^v \frac{c_i c_i'}{r_i}. \end{align*}\]
Theorem 6.5 (Orthogonal contrasts) When the number of replicates \(r_i\) is the same across treatment groups \(i\), if two contrasts \(c\) and \(c'\) are orthogonal, their estimates are uncorrelated.
Proof. When the number of replicates is \(r\) across all groups, then \[ \cov\left( \sum_{i=1}^v c_i \hat \tau_i, \sum_{i=1}^v c_i' \hat \tau_i \right) = \sigma^2 r \sum_{i=1}^v c_i c_i', \] and the sum is zero when the vectors are orthogonal.
Combined with a geometric interpretation of contrasts, this gives us an important result we will rely upon soon.
Theorem 6.6 (Basis for contrasts) By Definition 6.5, a contrast vector in an experiment with \(v\) treatments is a \(v\)-dimensional vector. Because of the constraint that \(\sum_i c_i = 0\), the contrast vectors span \((v - 1)\)-dimensional space.
We can hence form an orthogonal basis of \(v - 1\) contrast vectors, and any other contrast can be written as a linear combination of contrasts in that basis. This motivates Scheffé’s method for constructing a simultaneous 95% confidence interval for all possible contrasts (Definition 6.11).
We will return to contrasts in Chapter 7, when we see their many useful properties for estimation in multifactor experiments, and how those properties can guide our design.
6.5 Blocking
We can now consider blocked designs in linear models. We already know that blocking improves our experiments by increasing the power of tests and reducing the variance of estimates, but now we can see this through classic linear model theory, and the theory can give us much more specific guidance on how to design a blocked experiment.
We again consider a situation where the treatment units can be split into \(B\) blocks, where units within each group are expected to have more similar response values than units in different groups. If we have two blocking factors with \(B_1\) and \(B_2\) blocks, we could form \(B = B_1 B_2\) blocks. We choose the blocking factors based on the response variance between blocks.
6.5.1 The model
We’ve already seen a linear model for a blocked design in Example 6.3, but this model included an interaction. In classic experimental design, it’s common to start with a model that assumes purely additive effects: \[ Y_{hit} = \mu + \underbrace{\theta_h}_\text{block} + \underbrace{\tau_i}_\text{treatment} + \underbrace{\epsilon_{hit}}_\text{noise}, \] where \(h = 1, \dots, B\) indicates the block, \(i = 1, \dots, v\) indexes the treatments, and \(t \in \{1, \dots, r_{hi}\}\) indexes the experimental units within each block and treatment. An example layout is illustrated in Table 6.1. Typically we assume \(\epsilon\) is independent with variance \(\sigma^2\), and often we assume it’s normally distributed.
| Block | Treatment 1 | Treatment 2 | Total |
|---|---|---|---|
| 1 | \(r_{11}\) | \(r_{12}\) | \(r_{1 \cdot}\) |
| 2 | \(r_{21}\) | \(r_{22}\) | \(r_{2 \cdot}\) |
| 3 | \(r_{31}\) | \(r_{32}\) | \(r_{3 \cdot}\) |
| Total | \(r_{\cdot 1}\) | \(r_{\cdot 2}\) | \(n\) |
This looks just like a two-factor ANOVA, and indeed it is. It can be trivially rewritten in the conventional \(Y = X\beta + \epsilon\) linear model form. But remember that blocking is not just a way to analyze data—it is part of the design of the experiment, and affects how we assign treatments.
Exercise 6.7 (Blocked model to ordinary linear model) Consider the model \[ Y_{hit} = \mu + \theta_h + \tau_i + \epsilon_{hit}, \] where there are 3 blocks and 4 treatments. We can write an equivalent model in the form \(Y = X\beta + \epsilon\), where \(\beta\) is a vector of coefficients and \(X\) is a matrix of covariates.
How many columns will \(X\) have, and what do those columns represent?
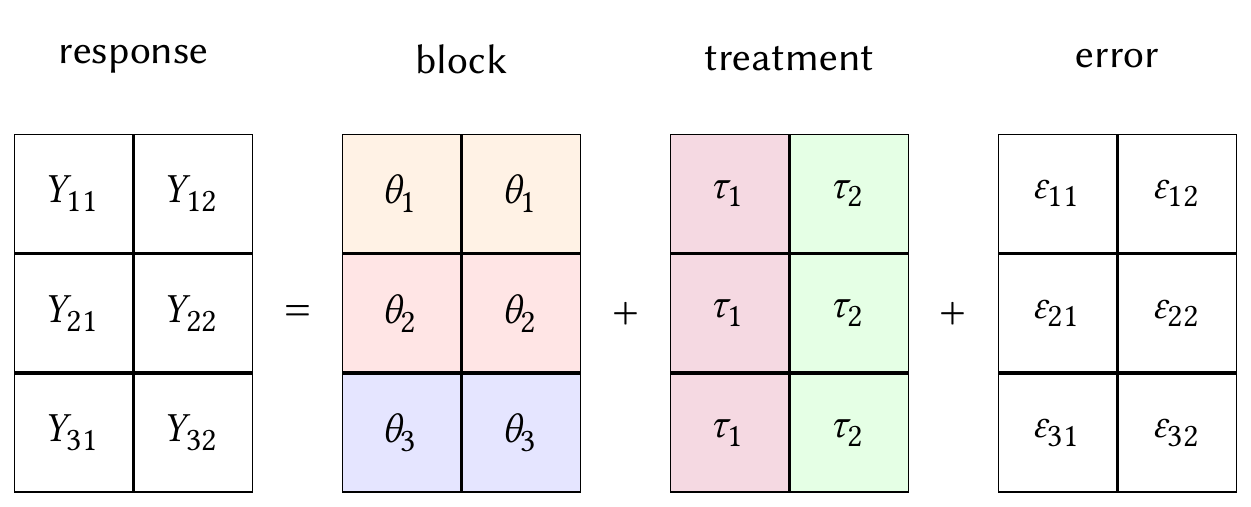
Though we’re including a blocking variable, the effect we are most interested in estimating is still the treatment effect; learning something about the blocking variable is just a bonus. Because we are fitting a model without interactions, the model decomposes the treatment and block effects in a structured fashion, as shown in Figure 6.1.
This decomposition ensures that regardless of block, the difference between treatment means is given by differences of \(\tau\). Our contrasts, then, are still linear combinations of treatment means \(\tau_i\).
Definition 6.6 (Contrasts in blocked designs) In a blocked model with additive effects as defined above, a contrast is a linear combination \[ \sum_{i=1}^v c_i \tau_i, \] where the contrast coefficients sum to 0. All contrasts remain estimable with ordinary least squares.
6.5.2 Types of blocked designs
To design a blocked experiment, we must choose the blocking variable, then determine \(r_{hi}\): the number of experimental units assigned to block \(h\) and treatment \(i\). We could select any numbers that fit within the sample size constraints of our experiment, but there are several properties of block designs that will guide our decisions.
Definition 6.7 (Complete block design) A complete block design is an experimental design in which each block contains at least one unit assigned to every treatment or treatment combination.
If some blocks are missing some treatment combinations, it is called an incomplete block design.
Our intuition is that a complete design should be better than an incomplete one. But if we do not have enough experimental units, we may not be able to conduct a complete experiment, so incomplete block designs can be valuable; they also allow us to use smaller blocks, which could be helpful to reduce variance, as we will see when we analyze the variance reduction gained by blocking.
Definition 6.8 (Balanced block design) Consider a blocked design with \(r_{hi}\) units assigned to block \(h\) and treatment \(i\). Such a design is balanced if the quantity \[ p_{ii'} = \sum_{h=1}^B \frac{r_{hi} r_{hi'}}{r_{h \cdot}}, \] where \(r_{h\cdot}\) is the total number of units assigned to block \(i\) across treatments, is constant for all treatment pairs \((i, i')\) (Mead, Gilmour, and Mead 2012, sec. 7.3).
To understand the benefit of balanced designs, we can break down the definition. The product \(r_{hi} r_{hi'}\) is the number of pairs of units in block \(h\) with treatment \(i\) or \(i'\)—that is, if you were conducting comparisons between every unit with treatment \(i\) and every other unit with treatment \(i'\), this is the number of comparisons you could make. It is divided by the total block size and summed across blocks, giving us a “sum of weighted concurrences” measuring the pairs of comparisons between treatments. If a design is balanced, then any pair of treatments \((i, i')\) has an equal sum, and hence an equal number of paired comparisons allowing us to compare the treatment means. When we conduct inference, we will see that balanced designs ensure pairwise comparisons between treatment means have equal precision (TODO ref future result).
Exercise 6.8 (Special balanced block designs) Show that the following special cases are balanced block designs.
- A design where \(r_{hi} = r\) for all blocks \(h\) and treatments \(i\), so every block contains an equal number of units assigned every treatment.
- A design where \(r_{h\cdot} = r\) for all blocks \(h\), so every block contains an equal number of units, and every pair \((i, i')\) of treatments occurs equally often across all blocks.
Finally, we can consider orthogonal designs, which have computational advantages.
Definition 6.9 (Orthogonal block design) Consider a blocked design with \(r_{hi}\) units assigned to block \(h\) and treatment \(i\). Such a design is orthogonal if \[ r_{hi} = \frac{r_{h\cdot} r_{\cdot i}}{n} \] for all block and treatment combinations \((h, i)\), where \(r_{h\cdot}\) is the total number of units in block \(h\), \(r_{\cdot i}\) is the total number of units assigned to treatment \(i\), and \(n\) is the total number of units in the experiment.
As we will see in the next section (TODO ref theorem/result), when an experiment is orthogonal its block and treatment effects can be separately estimated rather than requiring a multivariate regression. This had great advantages in the days before computers could fit multivariate regressions in milliseconds and drove many design decisions, but is much less important now.
TODO anything else
6.5.3 Estimation in blocked designs
As in a simple design without blocking, the treatment and block parameters \(\tau_i\) and \(\theta_h\) are not identifiable. However, the various TODO
TODO converting to \(\X\) and doing least squares
Theorem 6.7 (Contrasts in orthogonal blocked designs) In an orthogonal block designs, the contrasts (Definition 6.6) can be estimated as \[ \sum_{i=1}^v c_i \hat \tau_i = \sum_{i=1}^v c_i \bar Y_{\cdot i \cdot}, \] where \(\bar Y_{\cdot i \cdot}\) is the sample average over blocks and replicates.
Proof. TODO
6.5.4 Variance of blocked designs
If you’ve ever learned ANOVA the traditional way, you may have noticed how much it focuses on the partitioning of variance: breaking down the total variance in \(Y\) (the total sum of squares) into component parts, in the form of sums of squares attributed to various predictors. You may have wondered why we bother with that, because the sums of squares are not particularly useful in regression. But they do help us understand the benefit of certain experimental designs, which is perhaps why they have been taught for so long.
Recall that the prime quantity in ordinary least squares regression is the residual sum of squares, \[ \RSS = \sum_{i=1}^n (Y_i - \hat Y_i)^2, \] where \(\hat Y_i\) is the model’s prediction for observation \(i\). In this case, \[ \RSS = \sum_{h=1}^B \sum_{i=1}^v \sum_{t=1}^{r_{hi}} (Y_{hit} - (\hat \mu + \hat \theta_h + \hat \tau_i))^2, \] where \(r_{hi}\) is the number of replicates in block \(h\) and treatment \(i\). The residual sum of squares is one component of the total sum of squares, \[ \text{SST} = \sum_{h=1}^B \sum_{i=1}^v \sum_{t=1}^{r_{hi}} (Y_{hit} - \bar Y_{\cdot \cdot \cdot})^2, \] where a bar with a \(\cdot\) in a subscript indicates averaging over that subscript, rather than summing. The total sum of squares, then, is directly related to the variance of \(Y\).
In the special case of orthogonal designs (Definition 6.9), the relationship is a particularly nice one.
Theorem 6.8 (Decomposition of the squared error) In orthogonal designs, \[ \text{SST} = B \sum_{i=1}^v \sum_{t=1}^{r_{hi}} (\bar Y_{\cdot it} - \bar Y_{\cdot \cdot t})^2 + v \sum_{h=1}^B \sum_{t=1}^{r_{hi}} (\bar Y_{h \cdot t} - \bar Y_{\cdot \cdot t})^2 + \RSS. \] This is a little hard to think about, so consider the case when \(r_{hi} = 1\): \[ \text{SST} = B \underbrace{\sum_{i=1}^v (\bar Y_{\cdot i} - \bar Y_{\cdot \cdot})^2}_\text{treatment variation} + v \underbrace{\sum_{h=1}^B (\bar Y_{h \cdot} - \bar Y_{\cdot \cdot})^2}_\text{block variation} + \RSS. \]
In other words, in an orthogonal block design, the total variation in \(Y\) breaks down into three parts:
- Variation due to the treatment
- Variation due to the block
- Variation due to the error.
Exercise 6.9 (Prove it) Show the above identity by expanding out the definition of the total sum of squares, rearranging, and showing that the cross terms are 0. You may focus on the special orthogonal case where \(r_{hi} = r\) to simplify the arithmetic.
Why do we care about sum-of-squares arithmetic? Well, once we run an experiment, the total sum of squares is fixed. If we don’t block on anything, all of that variation must be accounted for by the treatment and by the residual error—so if we block on something, the residual error must go down.
Another way to think of it: if we fit a model without the blocking variable, but the true relationship is blocked, then in the new model, \[ Y_{it} = \tau_i + \underbrace{\epsilon_{it}}_{\theta_h + \epsilon_{hit}}. \] The error must account for the variation caused by the block variable and by any measurement error, noise, sampling variation, and so on.
As you know, the typical unbiased estimator for the error variance in a linear model is \[ \hat \sigma^2 = \frac{\RSS}{n - p}, \] where \(p\) is the number of (identifiable) parameters in the model. Blocking hence reduces \(\hat \sigma^2\). This affects our contrasts, the primary quantities of interest in an experiment.
Theorem 6.9 (Variance of contrasts in blocked designs) By Theorem 6.7, the variance of any contrast estimate in an orthogonal block design is \[\begin{align*} \var\left( \sum_{i=1}^v c_i \hat \tau_i \right) &= \sum_{i=1}^v c_i^2 \var(\bar Y_{\cdot i \cdot})\\ &= \sum_{i=1}^v c_i^2 \frac{\var(Y_i)}{r_{\cdot i}}\\ &= \sigma^2 \sum_{i=1}^v \frac{c_i^2}{r_{\cdot i}}, \end{align*}\] where \(r_{\cdot i}\) is the number of units assigned treatment \(i\) across all blocks.
Compare this to Theorem 6.1: A design without blocks has \(r_i\) units in treatment \(i\), whereas the blocked design has \(r_{hi}\) in each of \(B\) blocks, for \(r_{\cdot i}\) units in treatment \(i\). But because the blocked design will have a smaller \(\sigma^2\), it will most likely have a smaller \(\hat \sigma^2\), and hence will produce estimates of greater precision.
6.5.5 Selecting blocked designs
These results begin to give us guidance for designing an experiment with blocking variables. When designing a blocked experiment, we can choose:
- Which variables to block on
- How many units to assign to each block
- How many units to assign to each treatment in each block.
The first decision is relatively straightforward: If our goal is to estimate a treatment effect using a contrast, the variance of that estimate depends on \(\sigma^2\). According to the variance decomposition, the best way to reduce \(\sigma^2\) is to choose a blocking variable that maximizes \[ \sum_{h=1}^B \sum_{t=1}^r (\bar Y_{h \cdot t} - \bar Y_{\cdot \cdot t})^2, \] the squared variation in response between blocks. We should hence choose blocking variables we expect to be associated with high variation in the response variable.
The number of units per block may sometimes not be under our control—if we are blocking patients by age, it depends on how many patients in each group volunteer to join the study—but it frequently is. In an agricultural experiment where we want to test different crop varieties, we might have several fields and divide each field into small plots to plant each variety. The small plots are experimental units, while the fields form blocks, as there could be field-to-field variation in soil, sunlight, irrigation, and so on.
The number assigned to treatment in each block is also usually under our control, because we can assign the treatments. The exception is in cases when the blocks are too small to contain units in every treatment group. If our fields are split into five plots each, but there are eight treatments, each field can have at most five of eight total treatments.
6.6 Inference through ANOVA
In principle, if you’re familiar with the theory of inference in linear models, you know everything you need to know. Any model for a designed experiment can be written in the familiar \(Y = X \beta + \epsilon\) form of linear regression, and any contrast of \(\hat \tau_i\)s can be written as a combination of \(\hat \beta\)s. And we know how to do inference for \(\hat \beta\)—for example, see Section 5.3 of my regression notes.
But there is a great deal of specialized machinery for inference in experimental design, not because it is mathematically necessary but because it was computationally necessary. The machinery applies to special designs and not to arbitrary experiments, but the special cases often correspond to particularly desirable designs.
The computational necessity arose from the difficulty of calculating \(\hat \beta = (\X\T \X)^{-1} \X\T \Y\) in the days before computers. Once we have more than a few treatment and blocking factors, this requires doing large matrix multiplications, then inverting a large matrix, all by hand. Any further operation, such as producing confidence intervals for particular functions of \(\hat \beta\), requires even more matrix and vector operations.
By contrast,2 we will see that the special cases don’t require any matrix operations, and often make inference as easy as inference in a univariate regression.
6.6.1 The variance decomposition
As we saw in Theorem 6.8, the total sum of squares in an orthogonal experiment can be decomposed into components for the treatment and blocking factors. The theorem generalizes to cases with multiple treatment and blocking factors, provided the design remains orthogonal.
This suggests we can organize the crucial information in a table. Because we’re working with variances, this is Analysis of Variance, and the table is called an ANOVA table.
In an experiment with one treatment factor with \(v\) levels, one blocking factor with \(B\) levels, and \(n\) total units, the table is shown in Table 6.2.
| Variation | DF | Sum of squares | Mean square | Ratio |
|---|---|---|---|---|
| Block | \(B - 1\) | \(\text{SSB} = \sum_h r_{h\cdot} \bar Y_{h\cdot \cdot}^2 - n \bar Y_{\cdot \cdot \cdot}^2\) | \(\text{MSB} = \text{SSB}/(B - 1)\) | \(\text{MSB} / \RSS\) |
| Treatment | \(v - 1\) | \(\text{SSR} = \sum_i r_{\cdot i} \bar Y_{\cdot i \cdot}^2 - n \bar Y_{\cdot \cdot \cdot}^2\) | \(\text{MSR} = \text{SSR} / (v - 1)\) | \(\text{MSR} / \RSS\) |
| Error | \(n - B - v + 1\) | \(\RSS\) | \(\text{MSE} = \RSS/(n - B - v + 1)\) | |
| Total | \(n - 1\) | \(\text{SST}\) |
The “sum of squares” column makes sense following Theorem 6.8. It measures the amount of variation between blocks, between treatments, or due to error. But what about the other columns?
The DF is the Degrees of Freedom. There are many ways to think of this, but a good one is in terms of geometry. In this experiment, there are \(n\) observations of \(Y\). We can hence think of \(\Y\) as a vector in \(n\)-dimensional space. Now consider writing the model in the form \[ \Y = \X \beta + \epsilon, \] where \(\X\) is an \(n \times p\) design matrix, both \(\Y\) and \(\epsilon\) are \(n\)-vectors, and \(\beta\) is a \(p\)-vector, where \(p\) is the number of estimable parameters. We can break this matrix multiplication into pieces for the model components: \[ \Y = \mathbf{1} \mu + \X_\text{block} \theta + \X_\text{treat} \tau + \epsilon, \] where \(\X_\text{block}\) is a \(n \times (B - 1)\) matrix of block indicators and \(\X_\text{treat}\) is a \(n \times (v - 1)\) matrix of treatment indicators.
So we are expressing \(Y\) in terms of a basis consisting of the vector \(\mathbf{1}\), the columns of \(\X_\text{block}\), and the columns of \(\X_\text{treat}\). Then:
- \(\mathbf{1}\mu\) describes a 1-dimensional space (a line).
- \(\X_\text{block} \theta\) describes a \((B-1)\)-dimensional space spanned by the columns of \(\X_\text{block}\).
- \(\X_\text{treat} \tau\) describes a \((v - 1)\)-dimensional space spanned by the columns of \(\X_\text{treat}\).
- As the dimensions must add up to the dimension of \(\Y\), \(\epsilon\) describes the remainder, \(n - (B - 1) - (v - 1) - 1 = n - B - v-1\).
So the degrees of freedom correspond to the dimension of the space over which the term may vary. The mean square column divides the sum of squares by the degrees of freedom, producing an average per degree of freedom.
6.6.2 F tests
Because of the geometry, we can construct convenient hypothesis tests using the sums of squares. We can first consider overall tests: We may be interested in testing whether there is any treatment effect, via the null \[ H_0: \tau_i = 0 \qquad \text{for all treatments $i$}, \] or whether there is any block effect, via the null \[ H_0: \theta_h = 0 \qquad \text{for all blocks $h$}. \]
To construct a test we need a test statistic. The block and treatment sums of squares are natural starting points: SSB will be large if there are differences between block means and small otherwise, while SSR will be large if there are differences between treatment means and small otherwise. To derive a test, we need to know the distribution of the test statistic under the null.
Suppose we assume that the error \(\epsilon\) is normally distributed with fixed variance \(\sigma^2\) across all experimental units. When the treatment null is true, SSR is a sum of squared differences between a normally distributed random variable and its mean; the same goes for SSB when the block null is true. It is hence easy to show that \(\text{SSR}/\sigma^2 \sim \chi^2_{v-1}\), \(\text{SSB}/\sigma^2 \sim \chi^2_{B - 1}\), and \(\RSS/\sigma^2 \sim \chi^2_{n - B - v + 1}\) under the null.
Since the mean of each sum of squares depends on \(\sigma^2\), which varies between experiments and must be estimated, it makes sense to derive a test statistic whose distribution is independent of \(\sigma^2\). So we can divide by \(\RSS/\sigma^2\), producing the \(F\) statistic \[ F = \frac{\text{SSR}/(\sigma^2 (v - 1))}{\RSS/(\sigma^2 (n - B - v + 1))} = \frac{\text{SSR} / (v - 1)}{\RSS/(n - B - v + 1)}, \] which, under the null, has an \(F_{v - 1, n - B - v + 1}\) distribution. A similar test can be derived for SSB to test block effects.
If you squint at these tests long enough, you will see they are identical to nested \(F\) tests for linear models. That is, to test for the presence of a treatment effect, conduct the nested \(F\) test comparing a model with block and treatment effect to the reduced model with only a block effect, exactly the same way as any other nested \(F\) test. The interpretation is the same.
This derivation relies on the assumption of normality of the errors \(\epsilon\), which must be checked just as in other regression settings. It can be difficult to check in typical experiments, as experiments often have small sample sizes, making Q-Q plots and normality tests less useful. In larger samples, the central limit theorem ensures approximate normality, so checks are less important in exactly the settings where they are easier to conduct. Fortunately, experience has shown the \(F\) test to be fairly robust to non-normality, meaning the results are approximately correct even when the assumption is violated.
The crucial fact is that when the design is balanced, each of the subspaces mentioned above are orthogonal to each other. You will prove this in Exercise 6.11, and it will simplify estimation and inference.
TODO
6.6.3 Multiple testing
When we conduct an experiment with many treatment levels, there may be many contrasts of interest to us. The \(F\) test for treatment tests an overall null hypothesis, but we may also be interested in comparisons of specific combinations of contrasts. However, this can be risky.
Suppose we set \(\alpha = 0.05\) for our tests. We conduct \(k\) hypothesis tests. Suppose they are independent, and suppose the null hypothesis is true for every test. Then the probability of getting at least one significant result is one minus the probability of getting exactly zero significant results, so \[ \Pr(\text{one of $k$ is significant}) = 1 - (1 - \alpha)^k, \] This is graphed in Figure 6.2, showing that with even a modest number of contrasts, there’s a high risk of false positive results.

Now, depending on the contrasts, the tests may not be independent of each other, but that may just make the problem worse. If we are to run many contrasts, we must adjust our tests to keep our overall false positive rate controlled at a reasonable level. This overall rate is often called the “family-wise error rate”, since you are doing a “family” of related tests and want to control the overall error rate. There are several options.
6.6.3.1 Bonferroni correction
The Bonferroni correction is based on Boole’s inequality. If \(\Pr(A_i)\) represents the probability of some event \(A_i\), then \[ \Pr\left( \cup_{i=1}^k A_i \right) \leq \sum_{i=1}^k \Pr(A_i). \] That is: the probability that at least one event occurs is no larger than the sum of their probabilities. This inequality holds whether the events are independent or dependent.
Consequently, \[ \Pr(\text{one of $k$ is significant} \mid H_0) \leq k \alpha. \] To ensure the family-wise error rate is no larger than \(\alpha\), then, you must divide \(\alpha\) by \(k\). Use \(0.05/k\) when testing \(k\) contrasts, for instance, and the FWER should be no larger than 0.05.
This is known as the Bonferroni correction. It can be done either by reducing the significance threshold or by multiplying all \(p\) values in the study by \(k\) and using the original \(\alpha\) as the significance threshold. It can also be applied to confidence intervals to ensure they are joint confidence intervals.
The Bonferroni correction is conservative: It works regardless of the dependence between tests, and so it assumes the worst case. This means it is stricter than it has to be in specific situations, and results in lower power for tests. That’s why we often turn to procedures specifically derived for certain tests, as they can be more powerful while still controlling the FWER.
6.6.3.2 Tukey’s HSD
Sometimes we are only interested in pairwise comparisons between treatments: How does treatment 1 compare to treatment 2? What about treatment 4 versus treatment 7? Tukey proposed the “honestly significant differences” procedure that can produce confidence intervals and tests for all possible pairwise comparisons while still controlling the FWER.
Definition 6.10 (Tukey’s HSD) In a randomized experiment with \(v\) treatments, a \(1-\alpha\) confidence interval for \(\tau_i - \tau_j\) for \(i \neq j\) is \[ (\bar Y_{i \cdot} - \bar Y_{j \cdot}) \pm w_T \sqrt{\hat \sigma^2 \left( \frac{1}{r_i} + \frac{1}{r_j}\right)}, \] where \(r_i\) and \(r_j\) are the numbers of units in each treatment and \[ w_T = \frac{q_{v,n-v,1-\alpha}}{\sqrt{2}}, \] and \(q_{v,n-v,1-\alpha}\) is the \(1-\alpha\) quantile of the Studentized range distribution with \(v\) groups and \(n-v\) degrees of freedom. This confidence interval provides at least \(1 - \alpha\) coverage.
The distribution’s quantiles can be calculated with qtukey() in R.
Proof. For simplicity, consider the case where all treatments have \(r\) experimental units. Then define the statistics \(T_i = \bar Y_{i \cdot} - (\mu + \tau_i)\), which give the difference between the sample mean for treatment \(i\) and the population mean. If the errors are normally distributed, or if we believe the central limit theorem, these statistics will be (perhaps approximately) normally distributed. They are also independent. Then consider the statistic \[ Q = \frac{\max\{ T_i \} - \min \{T_i \}}{\sqrt{\hat \sigma^2 / r}}. \] Here we are taking the difference between the largest and smallest of \(v\) normally distributed random variables, and dividing by an estimate of the standard deviation. One can work out the distribution of this quantity, and it’s called the Studentized range distribution. Consequently, \[ \Pr(Q \leq q_{v, n-v, 1-\alpha}) = 1 - \alpha. \]
Now, how do we apply this to a particular comparison of two treatment means? If the largest difference between any \(T_i\) and \(T_j\) is \(|\max\{T_i\} - \min \{T_i\}|\), then it follows that any individual \(|T_i - T_j|\) must be less than or equal to that difference. Therefore, \[ \Pr\left(-q_{v,n-v,1-\alpha} \sqrt{\hat \sigma^2/r} \leq T_i - T_j \leq q_{v,n-v,1-\alpha} \sqrt{\hat \sigma^2/r}\right) \geq 1 - \alpha. \] We can hence define the confidence interval given in the definition.
Naturally, the intervals can be inverted to produce hypothesis tests for the pairwise differences, again controlling the family-wise error rate. Confidence intervals from Tukey’s HSD are less conservative (narrower) than Bonferroni intervals, and tests are more powerful.
6.6.3.3 Scheffé’s method
Scheffé (1953) introduced a method for constructing simultaneous confidence intervals for all possible contrast vectors.
Definition 6.11 (Scheffé’s method) In a randomized experiment with \(v\) treatments and \(r_i\) replicates per treatment, a \(1 - \alpha\) confidence interval for any contrast represented by contrast vector \(c\) is \[ \sum_{i=1}^v c_i \bar Y_{i \cdot} \pm \sqrt{(v - 1) F_{v-1,n-v, 1-\alpha}} \sqrt{\hat \sigma^2 \sum_{i=1}^v \frac{c_i^2}{r_i}}, \] where \(F_{v-1,n-v,1-\alpha}\) is the \(1-\alpha\) quantile of an \(F\) distribution with \(v-1\) and \(n-v\) degrees of freedom.
All such confidence intervals for an experiment will jointly have \(1 - \alpha\) coverage.
Proof. The proof is somewhat involved, but see Klotz (1969) for a simple proof in a special case.
Typically, these confidence intervals are the most conservative: Tukey’s HSD is specialized for only one set of possible contrasts, while Scheffé’s method must account for any possible contrast. The Bonferroni correction is less conservative provided you only do a few contrasts, but of course becomes more and more conservative the more tests or confidence intervals you construct.
6.7 Adding covariates: ANCOVA
We’re now ready to consider adding covariates to our experiments. Covariates are other measured features of the experimental units, beyond those we blocked on, that are expected to be associated with the response \(Y\).
Whenever possible, we would rather block on covariates. Blocking arranges the design matrix \(X\) in the most advantageous possible way; if we design carefully, we can achieve all the desirable properties of orthogonality described above. But it is not always possible to block on variables. Continuous variables, like age or household income, don’t naturally come in blocks—we would have to break them into discrete bins. Others may be hard to deliberately manipulate: When designing an industrial experiment, we can choose exactly how many samples to prepare with a certain chemical concentration, but when recruiting patients to a clinical trial, we cannot guarantee we’ll get exactly a certain number in each age range. We cannot randomize our patients so that equal numbers of them are age 21-30, 31-40, and so on.
For these covariates, or any others that are just inconvenient to block on, we can treat them as covariates. We can assemble a vector \(X_i \in \R^p\) for each unit \(i\) containing all the covariates, and assume a linear model: \[ Y_{hit} = \mu + \underbrace{\theta_h}_{\text{block}} + \underbrace{\tau_i}_{\text{treatment}} + \underbrace{\beta\T X_i}_{\text{covariates}} + \underbrace{\epsilon_{hit}}_{\text{noise}}. \] Such a model is known as “ANCOVA”, because it is ANOVA with covariates.
One can work out ANOVA tables for ANCOVA, following the template in Section 6.6.1. As there is no guarantee the covariates are orthogonal to anything, the useful geometric properties may not apply. With modern statistical software, there really is no point to write out full ANOVA tables. It’s easier to write the problem as a standard regression problem and apply the standard regression tools for testing and inference.
ANCOVA is typically done with linear models, but it does not have to be: if you believe \(X\) has a nonlinear relationship with \(Y\), you can write an appropriate nonlinear model. You could use polynomials and other transformations of \(X\), you could use splines, or in principle you could use fancy nonparametric and machine learning methods—anything that can estimate the relationship between \(X\) and \(Y\), provided you have enough data to fit it well.
In all cases, the benefit of adding covariates is similar to the benefit of blocking: it reduces the error variance by explaining some of the variation otherwise explained by \(\epsilon\). We estimate \(\var(\epsilon)\) in a linear model with \[ \hat \sigma^2 = \frac{\RSS}{n - p}, \] and if the covariates reduce the \(\RSS\) (more than increasing \(p\) with additional model terms reduces the denominator), using covariates will reduce \(\hat \sigma^2\) and hence produce narrower confidence intervals and more powerful tests.
6.8 Estimation in R
Now that we’ve seen the math, let’s consider how to analyze a designed experiment in R. Let’s use a real experiment and review how we fit the linear model, select the contrasts of interest, and produce confidence intervals and tests.
Example 6.4 (Resting metabolic rate) Dean, Voss, and Draguljić (2017) (example 10.4.1) present data collected by Bullough and Melby (1993), who conducted an experiment to compare different methods for measuring resting metabolic rate (RMR). Resting metabolic rate measures a person’s rate of energy consumption, and can be measured by carefully measuring the oxygen and carbon dioxide they breathe in and out; as the body consumes energy, it produces carbon dioxide, so the rate of production can be converted into energy use. Metabolic rate measurements are used in various medical and biological studies, but there was disagreement about the best way to measure resting rate: should the experimental subject spend the night in the laboratory, to be measured in the morning, or can they drive into the lab in the morning for the measurement? The extra activity may make them consume more energy, changing the measurements.
The experiment tested three methods:
- Inpatient, meal-controlled: The subject ate a meal provided by the experimenters, then was brought to the lab to stay the night before being measured in the morning.
- Outpatient, meal-controlled: The subject ate a meal provided by the experimenters, spent the night at home, and was driven to the lab in the morning for measurement.
- Outpatient: The subject ate their own meal at home, spent the night at home, and were driven to the lab in the morning for measurement.
The experiment used a within-subject design: There were 9 subjects, and they were measured all 3 ways in random order, on separate days.
The data is provided in resting.metabolic.rate.txt:
rmr <- read.table("data/resting.metabolic.rate.txt",
header = TRUE)
head(rmr) subject protocol rate
1 1 1 7131
2 1 2 6846
3 1 3 7095
4 2 1 8062
5 2 2 8573
6 2 3 8685The subject column identifies the subject (1 through 9), the protocol identifies the method (as numbered above), and rate is the measured resting metabolic rate in kJ/day.
It seems reasonable to think of this as an experiment with \(9 \times 3 = 27\) observations. We’d expect there to be lots of variation between subjects—people of different size, metabolism, age, and so on may have very different metabolic rates—and so it would be reasonable to block on size. Randomly ordering the measurements within subjects can be thought of as randomly assigning treatments within the blocks.
In principle, in R we can use the lm() function to fit the linear model, and translate between the \(\hat \beta\)s it estimates and the contrasts we’re interested in. But if we use aov() (for analysis of variance), we get the results presented in the standard ANOVA form.
Example 6.5 (ANOVA of Example 6.4) To fit the model and print the ANOVA table, we use aov() and summary() to get a nice table. The model formula is rate ~ subject + protocol: rate is the response, and we list both the treatment factor and blocking variable on the right hand side. But first we must make subject and protocol factor variables, so the numeric coding isn’t mistaken for a continuous variable.
rmr$subject <- factor(rmr$subject)
rmr$protocol <- factor(rmr$protocol)
fit <- aov(rate ~ subject + protocol, data = rmr)
summary(fit) Df Sum Sq Mean Sq F value Pr(>F)
subject 8 23117462 2889683 37.423 6.3e-09 ***
protocol 2 35949 17974 0.233 0.795
Residuals 16 1235483 77218
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1The tests suggest that the blocking factor (subject) is important and explains much of the variance in \(Y\), but the protocol does not. We might report this in text by saying:
The measurement protocol was not significantly associated with the resting metabolic rate measurement (\(F(2, 16) = 0.23\), \(p = 0.79\)).
Notice we’ve presented the \(F\) statistic, both degrees of freedom, and the \(p\) value. Always report results by giving a substantive interpretation, then the test statistic and \(p\) value that justify it.
Because aov() uses lm() underneath, the fit object is a special subclass of an lm fit:
class(fit)[1] "aov" "lm" This means it supports all the usual methods you use for linear models: residuals(), predict(), coefficients(), and, most importantly for us, vcov().
Of course, hypothesis tests are not our only goals. We may also want to make confidence intervals for specific contrasts.
Example 6.6 (Contrasts of Example 6.4) There are two ways to handle contrasts in R. In the first approach, we consider testing individual contrasts. We can use lm() to test the default contrasts, which compare each factor level to the first:
summary(lm(rate ~ subject + protocol, data = rmr))
Call:
lm(formula = rate ~ subject + protocol, data = rmr)
Residuals:
Min 1Q Median 3Q Max
-329.0 -191.7 24.3 131.0 514.3
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6975.04 177.37 39.325 < 2e-16 ***
subject2 1416.00 226.89 6.241 1.18e-05 ***
subject3 89.33 226.89 0.394 0.69898
subject4 400.67 226.89 1.766 0.09648 .
subject5 2061.67 226.89 9.087 1.02e-07 ***
subject6 198.00 226.89 0.873 0.39575
subject7 669.67 226.89 2.952 0.00938 **
subject8 2862.67 226.89 12.617 9.92e-10 ***
subject9 875.67 226.89 3.859 0.00139 **
protocol2 87.56 130.99 0.668 0.51341
protocol3 59.33 130.99 0.453 0.65667
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 277.9 on 16 degrees of freedom
Multiple R-squared: 0.9493, Adjusted R-squared: 0.9177
F-statistic: 29.98 on 10 and 16 DF, p-value: 1.786e-08The protocol2 and protocol3 rows correspond to the contrasts for \(\tau_2 -
\tau_1\) and \(\tau_3 - \tau_1\). We can view the coding R used using the contrasts() function:
contrasts(rmr$protocol) 2 3
1 0 0
2 1 0
3 0 1There are three rows, corresponding to the three levels. The columns are not contrast vectors in the sense of the coefficients \(c_i\); instead, they show how each factor level is represented in the design matrix \(X\) when R fits the model \(Y = X \beta + \epsilon\). We can see this explicitly using the model.matrix() function to view the \(X\) created for the model fit:
model.matrix(rate ~ protocol, data = head(rmr)) (Intercept) protocol2 protocol3
1 1 0 0
2 1 1 0
3 1 0 1
4 1 0 0
5 1 1 0
6 1 0 1
attr(,"assign")
[1] 0 1 1
attr(,"contrasts")
attr(,"contrasts")$protocol
[1] "contr.treatment"The protocol1 and protocol2 columns correspond to the columns returned by contrasts(), with the values chosen corresponding to the factor level of each experimental unit. We see that unit 1 was assigned protocol 1, unit 2 was assigned protocol 2, and unit 3 was assigned protocol 3.
We can change the contrasts by assigning to the contrasts() function:
contrasts(rmr$protocol) <- contr.sum(levels(rmr$protocol))The contr.sum() function produces “sum to zero” contrasts:
contrasts(rmr$protocol) [,1] [,2]
1 1 0
2 0 1
3 -1 -1Notice the columns here are explicitly constructed to be orthogonal to the intercept (a column of 1s). If your experiment has equal numbers of each protocol level, these columns of the design matrix would be orthogonal to the intercept column.
If we fit the model again, the coefficients and tests provided correspond to the two new contrasts:
summary(lm(rate ~ subject + protocol, data = rmr))
Call:
lm(formula = rate ~ subject + protocol, data = rmr)
Residuals:
Min 1Q Median 3Q Max
-329.0 -191.7 24.3 131.0 514.3
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7024.00 160.43 43.781 < 2e-16 ***
subject2 1416.00 226.89 6.241 1.18e-05 ***
subject3 89.33 226.89 0.394 0.69898
subject4 400.67 226.89 1.766 0.09648 .
subject5 2061.67 226.89 9.087 1.02e-07 ***
subject6 198.00 226.89 0.873 0.39575
subject7 669.67 226.89 2.952 0.00938 **
subject8 2862.67 226.89 12.617 9.92e-10 ***
subject9 875.67 226.89 3.859 0.00139 **
protocol1 -48.96 75.63 -0.647 0.52655
protocol2 38.59 75.63 0.510 0.61682
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 277.9 on 16 degrees of freedom
Multiple R-squared: 0.9493, Adjusted R-squared: 0.9177
F-statistic: 29.98 on 10 and 16 DF, p-value: 1.786e-08In the second approach, we can use the emmeans package, which supports multiple comparison procedures for contrasts. For example, the default pairwise contrast uses Tukey’s adjustment of the \(p\) values for all three pairwise contrasts.
library(emmeans)
fit_emm <- emmeans(fit, "protocol")
contrast(fit_emm, method = "pairwise") contrast estimate SE df t.ratio p.value
protocol1 - protocol2 -87.6 131 16 -0.668 0.7848
protocol1 - protocol3 -59.3 131 16 -0.453 0.8938
protocol2 - protocol3 28.2 131 16 0.215 0.9748
Results are averaged over the levels of: subject
P value adjustment: tukey method for comparing a family of 3 estimates 6.9 Exercises
Exercise 6.10 (Simple orthogonal block designs) Show that an experiment where \(r_{hi} = r\) for all blocks \(h\) and treatments \(i\) is an orthogonal block design (Definition 6.9).
We already showed that such a design is balanced in Exercise 6.8, so this simple design is complete, balanced, and orthogonal.
Exercise 6.11 (Geometry of experiments) You may know that linear regression can be thought of geometrically: in a linear model \(Y = X \beta + \epsilon\), with \(X\) an \(n \times p\) matrix of covariates, the least squares solution amounts to a projection of \(Y\) onto the column space of \(X\). That projection is \(\hat Y\), and \(\hat \beta\) gives its coordinates in the column space of \(X\).
Consider a balanced block design with a binary treatment and a binary blocking variable, so the linear model is \[ Y_{hit} = \mu + \theta_h + \tau_i + \epsilon_{hit}. \] There is no interaction, and there are an equal number of replicates (\(r\)) in each block-treatment combination.
- This model can be rewritten in \(Y = X \beta + \epsilon\) form by appropriately defining the columns of \(X\). State how many columns \(X\) will have and give a working definition for each column.
- Because there are only a few possible combinations of blocks and treatments, the design matrix is \(r\) repeats of a few rows. Write out these rows.
- Your design matrix \(X\) should contain a column for the blocks and a column for the treatment. These columns are correlated with the intercept/grand mean column. But we can make them orthogonal by using the Gram–Schmidt process. If you have two vectors \(u\) and \(v\), you can make them orthogonal by projecting one onto the other, and subtracting out the projection: \[ u' = u - \frac{u\T v}{v\T v} v. \] Use Gram–Schmidt to make the block and treatment columns orthogonal to the intercept/grand mean column. Write out the new design matrix.
- Are the new columns orthogonal to each other? Calculate their inner products.
- If the blocks were not balanced, would your result change? Why or why not?
Exercise 6.12 (Blocking in R) Return to the sim-crd.csv data file we introduced in Exercise 4.8.
Use your
completely_randomized()andblock_randomized()functions (from Exercise 4.6 and Exercise 5.3) to generate two datasets: One representing a completely randomized experiment on the data, and one representing a block-randomized experiment, blocking onprior_grade.Report:
- The estimated treatment effect in the completely randomized experiment, using Definition 4.2.
- The estimated treatment effect in the block randomized experiment, using Definition 5.3.
- The number of blocks in the blocked experiment and the number of units in each treatment in each block. Is this a balanced block design?
Use
aov()to fit two linear models: one to the completely randomized design, ignoringprior_grade, and one to the blocked design, usingprior_gradeas a variable in the analysis. Print the two ANOVA tables. Comment on the sums of squares:- Does
prior_gradeappear to account for much of the variance in the response? - Does the
assignmentrow change much between the two fits? In particular, consider the sum of squares and the \(F\) statistic: which do you expect to be different and why?
- Does
Repeat the fits using
lm()and examine the model summary. We’re particularly interested in the effect ofassignment. What is different in the estimates and standard errors between the two fits? Write a sentence interpreting the effect in the blocked model fit. Include a 95% confidence interval.
Exercise 6.13 (Defining contrasts) TODO extend Exercise 6.12 to ask for R code to set contrasts for desired quantities
Exercise 6.14 (Balanced block designs) In 2017, researchers discovered security vulnerabilities affecting every computer using common processor architectures (x86 in particular), in which standard processor features could be abused by attackers to get access to data that the operating system would not otherwise grant them access to. (Actually there were several related vulnerabilities, going under the names Meltdown and Spectre.)
Suppose you are an operating system manufacturer testing ways of protecting against the security vulnerabilities. You have two different possible mitigation strategies which you want to compare against an unprotected version. You’re worried that the mitigations may make software running on computers slower, and want to test various programs to see how fast they run with and without mitigations.
Different programs may be affected differently by the mitigations, so you decide to test five different programs under each of the three conditions: two different mitigations and the unprotected control version. You time how long each program takes to run. This time varies for various reasons, so you need to run each several times. But the programs are slow, and you only have time to make 45 total runs.
Describe the design you would use for this experiment. What are the blocks, what are the treatment groups, and how would you handle random assignment to ensure balance?
Let’s simulate some data. Below is the R function you should use to generate the data. It takes
mitigationandprogramarguments and returns the number of minutes taken to run that program with that mitigation, in one particular experimental run.# Simulate the run time of a mitigation for a particular program. # There are three mitigations: # 0: no mitigation # 1: one experimental mitigation strategy # 2: the other experimental strategy # There are five different programs, numbered 1 through 5. run_time <- function(mitigation, program) { 40 + 5 * mitigation + c(-8, 6, 14, -16, 4)[program] + rnorm(1, sd = 5) }Simulate data following the design you chose in part 1, recording the results into a data frame. Remember the constraint that you can only make 45 total runs, and remember to store the program and mitigation as factors, not numbers.
Note: Put your simulation code in a function so you can call it many times to get many simulated data frames. We’ll use this later in the problem.
Use
lmto estimate the effect of mitigation on runtime, ignoring the program variable entirely. Examine the standard errors reported bysummary. Now run a second model where you do include the program variable. What happens to the estimates and standard errors of the effect of the mitigations?(The
summaryfunction returns a list including acoefficientsmatrix containing the standard errors, if that’s helpful to you.)Use the
vcovfunction to get the covariance matrix of the estimates. What do you notice about the covariance between mitigation and program parameters?Now let’s examine an unbalanced design. Generate a data frame like you did in part 2, with the same number of rows, but this time do not enforce balance. Instead, for each observation, randomly pick a program and a mitigation. Fit the same models as before and examine the estimates, standard errors, and covariances again. What do you observe?
Of course, it’s hard to tell if differences in the standard errors are from this sample or are generic. Run 1,000 simulations from the balanced and unbalanced designs. For each simulation, fit the model with both mitigation and program factors, and record the standard errors on the mitigation coefficients. (Don’t include the intercept.) Report or plot your results. Calculate the average percent increase in standard error resulting from the unbalanced design.
Exercise 6.15 (When is blocking beneficial?) In Example 6.3, we considered having a binary treatment \(Z_i \in \{0, 1\}\) and a binary blocking variable \(X_i \in \{0, 1\}\). We can describe all possible cell means with the model \[ \E[Y_i \mid X_i, Z_i] = \beta_0 + \beta_1 Z_i + \beta_2 X_i + \beta_3 X_i Z_i. \] This corresponds to a table of cell means:
| \(Z_i = 0\) | \(Z_i = 1\) | |
|---|---|---|
| \(X_i = 0\) | \(\tau_{00} = \beta_0\) | \(\tau_{01} = \beta_0 + \beta_1\) |
| \(X_i = 1\) | \(\tau_{10} = \beta_0 + \beta_2\) | \(\tau_{11} = \beta_0 + \beta_1 + \beta_2 + \beta_3\) |
Suppose we conduct an experiment with \(r\) replicates in each cell, so there are \(n = 4r\) total experimental units. There are two reasonable estimators for the average treatment effect of \(Z\):
- Ignore blocking. Estimate \(\hat \tau_\text{noblock} = \bar Y_{\cdot 1} - \bar Y_{\cdot 0}\), where \(\bar Y_{\cdot 1}\) represents the average \(Y\) for the \(2r\) replicates with \(Z_i = 1\).
- Use blocking. Estimate \(\hat \tau_\text{block}\) using the blocked mean difference estimator, Definition 5.3.
These correspond to fitting linear models with only a \(Z\) term (\(\hat \tau_\text{noblock}\)) or with both \(X\) and \(Z\) (\(\hat \tau_\text{block}\)).
Assume that the variance of \(Y\) within each cell is \(\var(Y \mid X, Z) = \sigma^2\). Note that omitting \(X\) in the unblocked model means the variation due to \(X\) is absorbed in the error term—so the variance of the error in the unblocked model is not \(\sigma^2\).
- Derive a formula for \(\hat \tau_\text{block}\) in terms of \(\bar Y\).
- Calculate \(\var(Y \mid Z = 0)\) and \(\var(Y \mid Z = 1)\) in terms of the \(\beta\) parameters. Notice that \(\var(Y \mid Z) \neq \var(Y \mid X, Z)\). (Hint: Recall the law of total variance, and recall we have \(r\) replicates in each cell.) What does this imply about the variance of the errors in the unblocked model?
- Calculate \(\var(\hat \tau_\text{noblock})\) and \(\var(\hat \tau_\text{block})\).
- Consider \(\beta_2\) and \(\beta_3\), which together describe the influence of the blocking variable \(X\). Under what condition does \(\var(\hat \tau_\text{noblock}) = \var(\hat \tau_\text{block})\)? Which of \(\beta_2\) and \(\beta_3\) has the strongest effect on the variances?
Exercise 6.16 (Respiratory exchange ratio) In Example 6.4, we introduced the resting metabolic rate experiment. The experimenters also measured the respiratory exchange ratio of the subjects, which is the ratio between their production of carbon dioxide and consumption of oxygen. This gives an indication of which sources of energy in the body are being used, and is used in various exercise and stress tests.
The data is given in respiratory.exchange.ratio.txt. Load the data using read.table():
rer <- read.table("data/respiratory.exchange.ratio.txt",
header = TRUE)Because the data was collected as part of the same experiment, it has the same block design as in Example 6.4.
- Use
aov()to model respiratory exchange ratio, being sure to include the blocking factor. Print the ANOVA table. Comment on the sums of squares: does the blocking factor account for a lot of the variance? - Our inferences are based on the assumption that either (a) the errors are normally distributed or (b) the sample size is large enough that the central limit theorem ensures parameter estimates will be approximately normal. Evaluate option (a) by making a Q-Q plot of the residuals \(\hat
\epsilon_{ij}\). (You can use the
residuals()function to obtain these.) - Report the results of an \(F\) test for the null hypothesis that all measurement protocols have the same mean.
- Calculate all pairwise contrasts using the Tukey HSD method. Does your result match the result from part 3?