5 Reducing Variance
\[ \DeclareMathOperator{\E}{\mathbb{E}} \DeclareMathOperator{\R}{\mathbb{R}} \DeclareMathOperator{\var}{Var} \DeclareMathOperator{\cov}{Cov} \newcommand{\onevec}{\mathbf{1}} \newcommand{\X}{\mathbf{X}} \newcommand{\T}{^\mathsf{T}} \]
Now that we have considered simple experiments and simple estimators, we can consider the role of design in getting better estimates.
In regression, if you want better estimates, you’re used to considering different estimators. Worried about the variance of your predictions? Try ridge regression to penalize \(\hat \beta\). Worried whether the model is correct? Try models with splines, or smoothers, or interactions, or whatever; and use cross-validation to see which best explains the data.
But in designed experiments, our choice of design affects the bias and variance of our estimator. Choosing the right design ensures it’s unbiased, and some unbiased designs will have more or less variance than others. Choosing a good one, then, is like having more data: it lets us achieve precision with a sample of size \(n\) that another design might only obtain with a sample of size larger than \(n\).
5.1 Blocking
In many experiments, the experimental units are not all identical before the start of the experiment. They are, for example, real humans with different physical features, attitudes, behaviors, medical histories, and so on. Many of these attributes might be associated with their potential outcomes in complicated ways. These attributes are covariates, and if we can measure them, perhaps we can use them to help better estimate the treatment effect.
For example, consider an educational experiment. Our experimental units are students in a course, and we randomize them to two different lessons on experimental design. At the end of the lesson, we give them a test on the concepts covered. The goal is to determine which lesson better teaches the concepts. But of course the students may be different: some may have done better on previous homework assignments, some may have less experience with experimental design, and so on. If the covariate \(X_i\) represents student \(i\)’s previous homework grades, for instance, we might expect \(X_i\) to be positively associated with \(C_i(0)\) and \(C_i(1)\): a student already doing well in experimental design will probably do better on the test, regardless of lesson, than if they weren’t doing well on the homework.
Or, in other words: Because units have different covariates, and those covariates are associated with the response, the counterfactuals will have greater variance. According to Theorem 4.2, this increases the variance of our estimate \(\hat \tau\), making confidence intervals wider and tests less powerful.
It would be nice to reduce this variance and get more precise estimates. We have a few options:
- Conduct our experiments using only identical clones. Or, more realistically, select only units with certain covariate values, such as only students whose homework average is from 80 to 90%.
- Adjust for the covariates in the analysis. For example, use a regression model to account for their effect while estimating the treatment effect.
- Change how we design the experiment to ensure the two treatment groups are more similar.
Option 1 is not very practical—many experiments struggle to get sufficient sample size as it is, and ruling out many possible experimental units just makes that worse. We will return to option 2 later in the course (Chapter 6). Let’s consider option 3.
5.1.1 Blocked designs
Another way to think of the sampling variance problem is to consider randomization when the null hypothesis is true. If all our experimental units are identical clones and the sharp null is true, the treatment effect estimator should be essentially \(\hat \tau = 0\) regardless of who is randomized into the treatment group. But if the units are not identical, there will be some variance: sometimes the treatment group has more students with high grades, so \(\hat \tau > 0\), sometimes the control group has more students with high grades, so \(\hat \tau < 0\), and so on. And the variance is hence higher.
If that’s the problem, why not use the covariates during randomization to ensure the treatment and control groups have identical numbers of experimental units with particular values of the covariates?
There are a few ways to do this. One way is blocking.
Definition 5.1 (Blocking) Consider a randomized experiment with treatment indicator \(Z_i\) and a discrete covariate \(X_i \in \{1, \dots, B\}\). Then:
- Divide the \(n\) experimental units into \(B\) blocks, where block \(b\) contains all units with \(X_i = b\).
- Completely randomize the units within each block.
- Conduct the rest of the experiment as usual.
This ensures that each block is evenly split between each treatment level. For example, in the educational experiment, the covariate might be the current letter grade of the students, as shown in Table 5.1. Blocking ensures that A students are evenly split between treatment and control, B students are evenly split between treatment and control, and so on. It’s impossible for the control group to happen to get more C students in one randomization and more A students in another.
| Prior homework average | Lesson 1 | Lesson 2 |
|---|---|---|
| A | 30 | 30 |
| B | 30 | 30 |
| C | 20 | 20 |
| D | 10 | 10 |
5.1.2 Estimation in blocked designs
We can easily define a blocked version of the average treatment effect:
Definition 5.2 (Blocked average treatment effect) Let \(X_i \in \{1, \dots, B\}\) represent the block of unit \(i\), and let each block \(b\) have \(n_b\) units. The blocked average treatment effect is the average causal effect of treatment within one block: \[ \bar \tau_b = \frac{1}{n_b} \sum_{i : X_i = b} (C_i(1) - C_i(0)). \] These can be aggregated into the population ATE: \[ \bar \tau = \sum_{b=1}^B \frac{n_b}{n} \bar \tau_b. \]
This definition considers the average treatment effect within each block, then averages across blocks. It is easy to show that the blocked \(\bar \tau\) is identical to the original \(\bar \tau\) from Definition 4.1. What is different is the estimator this produces.
Definition 5.3 (Blocked mean difference estimator) To estimate the average treatment effect within each block, when the treatment \(Z_i\) is binary, we can use \[ \hat \tau_b = \frac{1}{n_{1b}} \sum_{i : Z_i=1, X_i=b} Y_i - \frac{1}{n_{0b}} \sum_{i : Z_i = 0, X_i = b} Y_i, \] where \(n_{0b}\) and \(n_{1b}\) are the number in each treatment in block \(b\). We can then aggregate across blocks to produce a blocked estimate: \[ \hat \tau = \sum_{b=1}^B \frac{n_b}{n} \hat \tau_b. \]
Exercise 5.1 (Bias of the blocked ATE) Show that the blocked mean difference estimator of Definition 5.3 is unbiased in a block randomized experiment.
This estimator matches the structure of a block randomized design: A blocked experiment is just several separate completely randomized experiments, one per block, so estimate each of those following Chapter 4, then combine the estimates according to the relative size of each block.
5.1.3 Variance in blocked designs
If a blocked design is just several completely randomized designs, and the estimator in Definition 5.3 is just a combination of mean difference estimators for completely randomized designs, it follows that we can calculate the variance of \(\hat \tau\) by combining several variances we already know how to calculate.
Theorem 5.1 (Variance of the ATE estimator in a blocked design) In a block randomized design with binary treatment and \(B\) blocks, the sampling variance of the mean difference estimator (Definition 5.3) is \[ \var(\hat \tau) = \sum_{b=1}^B \left(\frac{n_b}{n}\right)^2 \var(\hat \tau_b), \] where \(\var(\hat \tau_b)\) within each block is calculated according to Theorem 4.2: \[ \var(\hat \tau_b) = \frac{S_{0b}^2}{n_{0b}} + \frac{S_{1b}^2}{n_{1b}} - \frac{S_{01b}^2}{n_b}. \] Here \(n_b\) is the number of units in each block, \(n_{0b}\) and \(n_{1b}\) give the number in each treatment in that block, and \(S_{0b}^2\), \(S_{1b}^2\), and \(S_{01b}^2\) are the variances within the block, as defined in Theorem 4.2.
Proof. From Definition 5.3, we have \[\begin{align*} \var(\hat \tau) &= \var\left( \sum_{b=1}^B \frac{n_b}{n} \hat \tau_b \right)\\ &= \sum_{b=1}^B \var\left( \frac{n_b}{n} \hat \tau_b \right) \\ &= \sum_{b=1}^B \left( \frac{n_b}{n} \right)^2 \var(\hat \tau_b), \end{align*}\] because the estimates \(\hat \tau_1, \dots, \hat \tau_B\) within each block are independent.
To estimate the variance, then, we can repeat the same procedure: apply Theorem 4.3 within each block, then combine the results to obtain \(\widehat{\var}(\hat \tau)\). This requires that there be at least two units in each block so that we can calculate \(s_{0b}^2\) and \(s_{1b}^2\), the sample variances of the observed counterfactuals.
The next obvious question is: If we have \(n\) experimental units, which will estimate the ATE with lower variance, a completely randomized design or a block randomized design?
The answer is actually nontrivial. In most cases, if the counterfactuals vary between blocks, the blocked design will have lower variance for \(\hat \tau\); the effect is particularly strong if the counterfactual variance between blocks is large. Consider the following quantities:
- The average observed response in the control group, \(\frac{1}{n_0} \sum_{i : Z_i = 0} Y_i\)
- The average observed response in the treatment group, \(\frac{1}{n_1} \sum_{i : Z_i = 1} Y_i\)
- The true individual treatment effects, \(C_i(1) - C_i(0)\), and their average \(\bar \tau\).
Suppose \(\bar \tau = 0\), and suppose there is a blocking variable \(X_i \in \{0, 1\}\) such that when \(X_i = 1\), both counterfactuals are 1 unit higher than when \(X_i = 0\). This means \(X_i\) is not associated with the treatment effects, but if the treatment group happens to contain more units with \(X_i = 1\) than the control group, \(\hat \tau > 0\). If the reverse happens, \(\hat \tau < 0\). The sampling variation in the number of \(X_i = 1\) units assigned to each treatment group creates sampling variation in \(\hat \tau\).
You’ll explore this phenomenon in a concrete example in Exercise 5.4. It leads to the general advice to block whenever you can, because blocking almost always reduces the estimation variance. In rare and strange cases, it can raise the variance—see Pashley and Miratrix (2022) for an extended discussion—but generally, if you know the blocking variable is associated with the response, you should block on it.
5.1.4 Inference in blocked designs
Inference for \(\bar \tau\) in blocked designs proceeds very similarly as it does in completely randomized designs.
To test the sharp null hypothesis, we can again use a randomization test. We use the same procedure as in Definition 4.7: Repeatedly re-randomize the treatment assignments and calculate the test statistic. The only difference is that every randomization is a block randomization, not a complete randomization, so the test statistic should have lower variance. This increases the power of the test.
Similarly, we can construct confidence intervals and tests for \(\bar \tau\) following the same procedures as described in Section 4.6, but using our blocked estimate of the variance (Theorem 5.1) rather than the original estimator. This should produce narrower confidence intervals and more powerful tests.
5.1.5 Extending block designs
So far we have considered blocking on a single categorical variable: each unit has a covariate \(X_i \in \{1, \dots, B\}\), and so we form \(B\) blocks. But in a well-designed experiment, we may know many things about each unit before randomization, and several of them may be associated with the counterfactuals. We can use them all in blocking: if we have one variable with \(B_1\) categories and another with \(B_2\) categories, we can form \(B_1 \times B_2\) blocks, each representing a unique combination of blocking variables. The only limitation is that we must have enough experimental units to ensure each combination has several units.
We may also have continuous variables, not just discrete categorical variables. Can we extend blocked designs to these situations? Certainly: just discretize the variables into bins, then block on the bins. Provided units with similar numerical values have similar responses, this will ensure similar units are equally balanced between treatment and control.
5.2 Covariate balance
If blocking is about ensuring that the treatment and control groups are as similar as possible, apart from their treatment, it seems like we could ensure that in other ways. First, and most obviously, we could check the “success” of the randomization: After randomizing, we could check the covariate distributions within each group and determine if they are similar.
If you read medical and psychological papers describing experiments on humans, you’ll often see this done. These papers often have a table summarizing the demographics of the subjects—age, gender, education, socioeconomic status, and whatever medical or psychological covariates are relevant—overall and by treatment group. In fact such tables are so common that they are often referred to as “Table 1”, since it feels like every paper has a Table 1 giving the covariate balance for the treatment groups.
In fact, I opened the latest edition of PLOS Medicine and found the first paper with “trial” in its name, and Table 1 in that paper is titled “Participant baseline characteristics, by study arm”—see Figure 5.1. This study had three treatment levels and covariates including age, sex, education, employment status, household size, poverty index, and various medical measures and tests.
Even if we block on some of these covariates (such as sex and education), there are many other covariates, and it is impractical to block on all of them—there would be too many unique combinations, too many blocks, and not enough patients per block.
But perhaps there is another way. If we devise a way to measure how balanced the covariates are, can we just randomize repeatedly until they’re balanced enough?
5.2.1 Measuring covariate balance
Tables like those in Figure 5.1 can show us whether covariates are, on average, balanced between treatment groups. But it would be helpful to devise a quantitative score that tells us exactly how unbalanced the covariates are.
Let \(\X\) be an \(n \times p\) matrix of covariates for all \(n\) experimental units. Suppose the units are divided into two treatment groups indicated by \(Z_i \in \{0, 1\}\), and define \[\begin{align*} \bar X_{j,0} &= \frac{1}{n_0} \sum_{i : Z_i = 0} \X_{ij}, & \bar X_{j,1} &= \frac{1}{n_1} \sum_{i : Z_i = 1} \X_{ij}. \end{align*}\] These represent the average values of covariate \(j\) in the control and treatment groups.
Definition 5.4 (Standardized covariate mean difference) The standardized covariate mean difference \(d_j\) for covariate \(j\) is defined to be \[ d_j = \frac{\bar X_{j,1} - \bar X_{j,0}}{s_j}, \] where \[ s_j = \sqrt{\frac{s_{j,1}^2 + s_{j,0}^2}{2}} \] is the pooled standard deviation, based on \(s_{j,1}^2\) and \(s_{j,0}^2\), the variance of covariate \(j\) within the treatment and control groups.
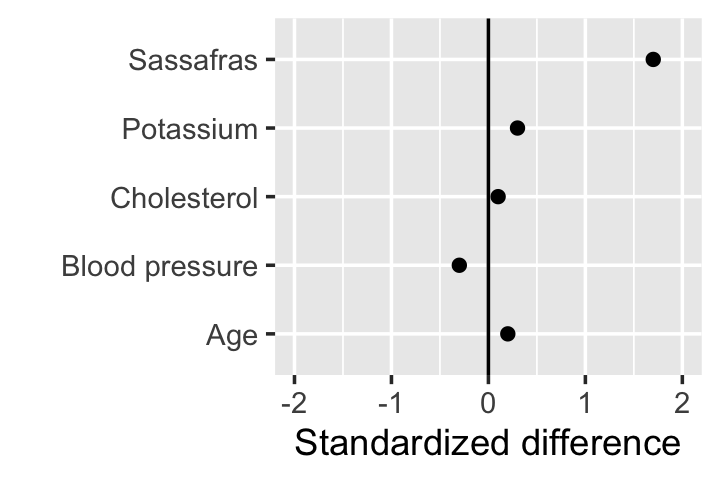
We can interpret the standardized covariate mean difference like a \(z\) score: if \(d_j = 1\), the value of covariate \(j\) is about 1 standard deviation higher in treatment group 1 than it is in treatment group 0. We could make a table of the standardized covariate mean differences for all the covariates, but it’s easier to make plots, as shown in Figure 5.2.

These plots are useful to visually assess covariate balance, but we’d like an automated procedure to ensure balance. Rather than the standardized covariate mean difference, which measures the “distance” between treatment and control groups one covariate at a time, we’d like a single distance metric for all the covariates. One convenient metric is the Mahalanobis distance.
Definition 5.5 (Mahalanobis distance) The Mahalanobis distance between two vectors \(x, y\) in \(\R^p\) relative to a distribution with variance matrix \(\Sigma \in \R^{p \times p}\) is \[ \delta_M(x, y) = \sqrt{(x - y)\T \Sigma^{-1} (x - y)}. \]
When \(p = 1\), this reduces to the \(z\) score; for \(p > 1\), it scales each dimension according to its variance (and the covariance between dimensions) to account for their differing variances. We can apply the Mahalanobis distance to the covariate mean differences.
Definition 5.6 (Mahalanobis distance of mean differences) To measure the covariate balance between two treatment groups, let \(\bar \X_0\) and \(\bar \X_1\) represent the mean covariate vectors in each treatment group. We can define the Mahalanobis distance \[\begin{align*} d &= \sqrt{(\bar \X_1 - \bar \X_0)\T \var(\bar \X_1 - \bar \X_0)^{-1} (\bar \X_1 - \bar \X_0)}\\ &= \sqrt{\frac{n_1 n_0}{n} (\bar \X_1 - \bar \X_0)\T \widehat{\var}(\X)^{-1} (\bar \X_1 - \bar \X_0)}, \end{align*}\] where \(\var(\bar \X_1 - \bar \X_0)\) is the population variance under repeated randomization of \(Z\) and \(\widehat{\var}(\X)\) is the sample variance matrix of \(\X\).
Exercise 5.2 (Alternative definitions) Show that the two formulas in Definition 5.6 are equivalent.
Hint: We can write \[ \bar \X_1 = \frac{1}{n_1} \X\T Z, \] where \(Z\) is the vector of treatment assignments. Use a similar form for \(\bar \X_0\) to write \(\bar \X_1 - \bar \X_0\) in terms of \(\X\).
Further hint: Recall that if \(A\) is a fixed matrix and \(Y\) is a random vector, \(\var(AX) = A \var(Y) A\T\).
Even further hint: Recall that in Exercise 4.5, you worked out the variance matrix \(\var(Z)\).
This gives us a single number to measure the difference in mean covariate values between treatment groups, appropriately accounting for the variance and covariance of the covariates.
But suppose we plan an experiment, perform the randomization, and find the Mahalanobis distance between groups is large. What can we do about it?
5.2.2 Rerandomization
Intuitively, a simple answer is “Randomize again.” If the randomization resulted in a large imbalance, we know this will affect the treatment effect estimates, so skip that randomization and try again. This has been informally done for decades, going back to R. A. Fisher; Donald B. Rubin recounts asking his PhD advisor, William G. Cochran, this question in the 1960s:
What was his advice if, in a randomized experiment, the chosen randomized allocation exhibited substantial imbalance on a prognostically important baseline covariate? According to my memory, his reply had two layers: (1) WGC: Why didn’t you block on that variable?; DBR: Well, there were many baseline covariates, and the correct blocking wasn’t obvious; and I was lazy at that time; and (2) WGC: This is a question that I (WGC) once asked Fisher (RAF), and RAF’s reply was unequivocal. Recreated (hearsay via WGC) RAF: Of course, if the experiment had not been started, I would rerandomize. (Rubin 2008)
But the formal design and analysis of rerandomized experiments was not studied until recently. Analyzing a rerandomized experiment as though it were an ordinary completely randomized or block randomized experiment will give invalid tests and confidence intervals—the procedures we have described so far consider the distribution of estimators and test statistics under repeated randomization, and using rerandomization means some randomizations are unused.
Lock Morgan and Rubin (2012) proposed a way to correctly analyze rerandomized experiments. Their procedure (pp. 1265-66) is:
- Collect covariate data.
- Specify a balance criterion determining when a randomization is acceptable.
- Randomize the units to treatment groups.
- Check the balance criterion; if the criterion is met, go to Step 5. Otherwise, return to Step 3.
- Conduct the experiment using the final randomization obtained in Step 4.
- Analyze the results using a randomization test, keeping only simulated randomizations that satisfy the balance criterion specified in Step 2.
Step 6 contains the key change: our randomization tests (Definition 4.7) must consider covariate balance, estimating the null distribution of the test statistic among balanced randomizations. The benefit of randomization tests is that this is a fairly easy change to make, though of course it makes the test even slower to run.
Rerandomization is an active research area, as there are many possible ways to define covariate balance beyond the Mahalanobis distance, many things we might try to do besides test sharp nulls, and many more complicated designs we might run, and it’s not yet clear the best way to rerandomize in every possible case.
5.3 Exercises
Exercise 5.3 (Generating a block randomized design) In Exercise 4.6, you wrote a completely_randomized() function to generate a completely randomized design. Now we need a block_randomized() function to do the same for a block randomized design, with the following signature:
#' @param population Data frame of `n` experimental units, containing their
#' covariates and potential outcomes.
#' @param blocking_var String naming a column in `population` to block on. Each
#' unique value of this column will form a block.
#' @param levels Number of treatment levels.
#' @return Data frame with an `assignment` column, containing integers 1, ...,
#' levels, representing the level to which each unit is assigned.
block_randomized <- function(population, blocking_var, levels) {
# TODO fill in
}You may assume the number of units in each block is greater than or equal to the number of treatment levels, but it need not be an integer multiple of the number of levels. You may assign (roughly) equal numbers of units to each treatment group.
Hint: You can call completely_randomized() from within block_randomized() to do much of the work.
Exercise 5.4 (Variance of the ATE in blocked designs) In Exercise 4.8, you loaded a simulated dataset providing both potential outcomes for \(n = 100\) experimental units—students in a statistics course, to be specific. You found the true population average treatment effect \(\bar \tau\) and simulated a completely randomized experiment and a randomization test for the sharp null.
But the dataset contained two covariates giving pre-treatment information about the students:
crd <- read.csv("data/sim-crd.csv")
head(crd) prior_grade year treatment1 treatment2
1 A junior 12.017082 9.365763
2 C junior 3.623687 4.558320
3 A junior 8.811771 10.844473
4 A junior 9.834920 7.593980
5 A junior 11.143657 10.058124
6 B sophomore 8.372420 7.992201Let’s explore using blocking to improve our estimates.
In Exercise 4.8, you calculated \(\hat \tau\) in the completely randomized design by using
completely_randomized()andobserve(). Do this again, but repeat it 1,000 times and calculate the variance and standard deviation of the estimates you obtain. This lets you estimate \(\var(\hat \tau)\).Verify your variance against the true sampling variance of the mean difference estimator, given in Theorem 4.2. (You have the counterfactuals, so you can calculate this exactly.) Does the variance match?
Now consider running a block randomized experiment. In Theorem 5.1, we worked out the variance of the ATE estimator in blocked designs. Calculate this variance for
- an experiment blocked by
prior_grade, and - an experiment blocked by
year.
Which is the better blocking variable?
- an experiment blocked by
Using the variable you selected in part 3, and using your
block_randomized()function from Exercise 5.3, conduct a block randomized experiment. Calculate your estimate of the average treatment effect using Definition 5.3.Now conduct a randomization test for the sharp null hypothesis, again using the blocking variable you selected and using \(|\hat \tau|\) as the test statistic. Report the \(p\) value of the test. What do you conclude about the null hypothesis?
Finally, as you did in part 4 of Exercise 4.8, estimate the power of the test. How does it compare to the power of the test in the completely randomized design?
Exercise 5.5 (Blocking an educational experiment) Return to the ACID study of Exercise 3.1. Suggest three possible blocking variables for this study.