9 Response Surfaces

So far, we have considered experiments where the goal is to estimate treatment means or mean differences. But as we discussed in Chapter 3, that is not the only possible goal for an experiment.

Suppose we have $p$ treatment factors, each of which is a continuous variable. In principle, the value of the mean response at each possible combination of factors forms a surface in $(p + 1)$-dimensional space. We can call this a response surface.

We can express the possible goals of an experiment in terms of the shape of that surface. So far, we have considered experiments to find the difference in response between specific points on that surface. But what if we want to learn the shape of the surface more generally, for instance so we can find the maximum?

We can easily imagine situations where finding a maximum is desirable:

The treatment factors are parameters for some chemical production process—input concentrations, temperature, pressure, and so on. The response is the efficiency of the process. We’d like to find the most efficient way to run the chemical plant.
The treatment factors are parameters for YouTube’s video recommendation algorithm. The response is the “engagement” of users, measured by how many videos they watch, how long they watch, how many ads they click on, or some other metric that product managers decide is interesting. We’d like to make people spend the maximum possible amount of their lives glued to their phones.
The treatment factors are doses of various medications. The response is the fraction of tumor cells (in a test tube) that die when exposed to the medications. We’d like to find a combination of cancer drugs that cause the strongest effect on tumors.

You can undoubtedly think of many other examples where we want to optimize something by controlling various factors.

The simplest way to achieve these goals is to try lots and lots of combinations of the factors, then pick the best one according to the estimated treatment means. But these are continuous variables, so the space of possible combinations is large, and making a grid across the entire space might entail testing millions of combinations. How can we do better?

We might start by treating this as a numerical optimization problem. There is some unknown function $f(x_1, x_2, \dots, x_p)$ that produces the response as a function of the $p$ factors. We do not know $f$, so we cannot solve for its maximum. But perhaps we believe that $f$ is reasonably smooth, so we can learn something about its shape by evaluating it at well-chosen points. We could proceed iteratively instead: start with a guess, then figure out what changes would increase the response, repeating the process until the response has increased to a local maximum.

9.1 Optimization in general

You’re probably already familiar with a few numerical optimization techniques. Let’s consider a couple examples.

First, there are first-order optimization methods. “First-order” means they use the function’s value and its derivative at a point, but no other information about it. Perhaps the most famous first-order method is gradient ascent.

Definition 9.1 (Gradient ascent) Consider maximizing a function $f : \R^p \to \R$. Start with an initial guess $x^{(0)} \in \R^p$. Then, for steps $k = 1, 2, \dots$ until convergence, update the guess with \[ x^{(k + 1)} = x^{(k)} + \gamma \nabla f(x^{(k)}), \] where $\gamma > 0$ is a step size and $\nabla f(x^{(k)})$ is the gradient, the vector of partial derivatives of $f$ evaluated at $x^{(k)}$.

This procedure is called gradient ascent. If the step size $\gamma$ is chosen well, it will converge to a (possibly local) maximum of $f$.

We can interpret gradient ascent as a simple procedure: Guess $x$, find the slope of $f$ at $x$, then move $x$ in the direction of steepest ascent. Repeat until the slope is basically flat.

First-order methods are widely used—you’re probably familiar with gradient descent, which is just gradient ascent but for minimization. It is spectacularly common for training neural networks, and indeed is so popular that you might forget there are any other ways to do it.

But there are second-order optimization methods as well. A common one is Newton’s method.

Definition 9.2 (Newton’s method for optimization) Consider maximizing a function $f : \R^p \to \R$. Start with an initial guess $x^{(0)} \in \R^p$. Then, for steps $k = 1, 2, \dots$ until convergence, update the guess with \[ x^{(k + 1)} = x^{(k)} - \left( \nabla^2 f(x^{(k)}) \right)^{-1} \nabla f(x^{(k)})\T, \] where $\nabla^2 f(x^{(k)})$ is the matrix of second partial derivatives of $f$ evaluated at $x^{(k)}$.

Newton’s method amounts to approximating $f$ with a quadratic, defined according to the first and second derivatives of $f$, and then updating our guess to the maximum of that quadratic. No step size parameter is required.

In general, optimization methods like these work well when $f$ is well-behaved: when it is differentiable and, ideally, convex. If $f$ has numerous local maxima, no numerical optimization method will provide a guarantee that regardless of the starting point $x^{(0)}$, the optimizer will find the global maximum and not just a local maximum.

9.2 First-order response surface designs

First-order response surface designs apply the basic idea of gradient ascent to a function $f$ whose value $f(x)$ and gradient $\nabla f(x)$ can only be approximated by running an experiment. Suppose our response variable $Y$ is related to the treatment factors $X$ by $Y = f(X) + \epsilon$, and we would like to find \[ x^* = \argmax_x f(x). \] The iterative optimization approach suggests we should zoom in on the surface $f(x)$. Rather than trying to learn the entire shape of $f$ from a single experiment, such as by doing a huge factorial experiment over the entire range of every treatment factor, we pick a starting value $x^{(0)}$. We then try to estimate $\nabla f(x^{(0)})$ by doing a local experiment that changes $x$ slightly to estimate the gradient at $x^{(0)}$.

[TODO diagram of a 3D response surface, showing us zooming in and fitting a plane to a small part]

After we estimate $\nabla f(x^{(0)})$, we apply the update rule in Definition 9.1, then repeat for each $x^{(k)}$. Estimating $\nabla f(x^{(k)})$ is the essential part: the gradient tells us how to change $x^{(k)}$ to optimize the function.

9.2.1 Desirable properties

Given our iterative optimization approach, our design need only produce an estimate of $\nabla f(x)$; the model can be as simple as possible as long as it can give us the gradient. It follows that we can use the Taylor approximation of $f(x)$: \[ f(x) \approx f(x^*) + \nabla f(x^*)\T (x - x^*). \] This approximates $f(x)$ as a linear function of $x$, so evidently a simple linear model will suffice. The slope coefficients $\beta$ determine the gradient.

We can thus determine that an experimental design for response surface modeling should:

Give us the best possible estimate of $\nabla f(x^{(k)})$ given a fixed number of experimental units
Or, to make that precise, have the lowest possible variance of the slope estimates $\hat \beta$
Let us estimate $\hat \sigma^2$, so we can tell if the linear approximation fits well

We can elaborate the second criterion further. A reasonable objective would be to minimize the average variance of the regression coefficients, \[ \frac{1}{p + 1} \sum_{i=0}^p \var(\hat \beta_i) = \frac{1}{p + 1} \trace(\var(\hat \beta)). \] One can show that when the treatment factors are centered and scaled, this objective is minimized when the columns of the design matrix $\X$ are orthogonal (Exercise 9.3). This suggests using factorial designs and their variations.

9.2.2 Standard first-order designs

Consider a situation where $p = 2$, so we can draw the design space in 2D:

[TODO diagram]

Objective 1 suggests we should use a design with four combinations of the two treatment factors, meaning a factorial design (Section 7.1) or fractional factorial design (Section 7.5). [TODO draw]. Objective 3 suggests we need more than one replicate at one or more design points, so we can estimate $\hat \sigma^2$; but putting a replicate at only one design point makes the design not orthogonal, while putting replicates at every design point means doubling or tripling the sample size.

So we add a center point. [TODO draw]. The center point has $n_0$ replicates, typically somewhere between 3 and 6. This design is now called a “standard first-order design.” With the center point, the design matrix can still be written in orthogonal form. If we rescale the variables so their largest and smallest values are $\pm 1$ and the center point is at 0, the design matrix is \[ \X = \begin{pmatrix} 1 & -1 & -1\\ 1 & -1 & +1\\ 1 & +1 & -1 \\ 1 & +1 & +1 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \\ \vdots & \vdots & \vdots \end{pmatrix}. \] We can see that the two factor columns are indeed orthogonal. And if we fit the linear model $Y = f(X) + \epsilon = X \beta + \epsilon$, where $\beta = (\beta_0, \beta_1, \beta_2)$, then \[ \nabla f(X) = \begin{pmatrix} \beta_1 \\ \beta_2 \end{pmatrix}, \] so we may trivially estimate the gradient using $\hat \beta$. We then plug the estimate into Definition 9.1 to find the next center point and repeat the procedure.

A full factorial first-order design has $2^p + 1$ design points, where $p$ is the number of treatment factors. With $n_0$ replicates at the center point, this requires $2^p + n_0$ observations. We can reduce this by using fractional factorial designs (Section 7.5), provided the main effects are not aliased with each other. Response surface designs are frequently used in industrial settings where the error $\sigma^2$ is low, so it is common to have no replicates ($r = 1$) and conduct a fractional factorial design.

9.2.3 Testing for lack of fit

The general intuition is that when $x^{(k)}$ is far from the maximum, a linear model is probably a good approximation of $f$. It at least tells us the direction of steepest ascent. As $x^{(k)}$ gets close to the maximum, the curvature may become more important—if we imagine a nice convex function, it looks fairly quadratic near the maximum, not linear.¹

This suggests we need a way of testing whether a first-order approximation is sufficient, or whether a second-order approximation is necessary. Your first guess may be a partial $F$ test: fit a linear model and then a model with quadratic terms, and test the null hypothesis that the quadratic coefficients are zero.

But unfortunately you will find that the quadratic terms are aliased in this design. They can’t be separately estimated, so you can’t do the obvious $F$ test. The problem is simply the number of parameters. For example, when $p = 2$, a full quadratic model has 6 parameters (intercept, two linear terms, two quadratic terms, and the interaction); but the number of unique design points is $2^p + 1 = 5$, so the design matrix has only 5 unique rows, regardless of the number of center point replicates. The design matrix is not of full rank, so there is not a unique solution to the least-squares problem. Or, in other words, the design matrix is necessarily collinear.

However, it is still possible to obtain $\hat Y$, the vector of fitted values, in a linear model with a collinear design matrix. (See the 707 lecture notes, section 9.5.) We can hence still calculate the residual sum of squares (RSS) for the quadratic model and compare it to the RSS for the linear model using a standard partial $F$ test. However, the parameters of the partial $F$ test’s null distribution depend on the number of parameters and degrees of freedom, which are tedious to work out when the model is not of full rank, so it is easier to understand the test when it’s worked out differently.

A partial $F$ test takes the ratio of the change in RSS due to using the larger model over the RSS of the larger model, each scaled by their respective degrees of freedom. Here, the RSS of the larger model is called the sum of squares for pure error. The larger model will fit the factorial points perfectly, so only at the center point (where there are replicates) is there error. Hence we calculate \[ \text{SS}_\text{PE} = \sum_{\text{$i$ at center point}} (Y_i - \bar Y_\text{center})^2, \] the sum of squares for the observations at the center point. This has $n_0 - 1$ degrees of freedom. The residual sum of squares of the first-order model, $\RSS_\text{FO}$, has $n - p - 1$ degrees of freedom. Here $n = n_d + n_0 - 1$, where $n_d$ is the number of unique design points, so the $F$ statistic is hence \[ F = \frac{(\RSS_\text{FO} - \text{SS}_\text{PE}) / (n_d - p - 1)}{\text{SS}_\text{PE} / (n_0 - 1)}. \] Under the null this follows the $F_{n_d - p - 1, n_0 - 1}$ distribution. When the first-order model fits poorly, $\RSS_\text{FO}$ is large, causing the $F$ statistic to grow and causing the null to be rejected. Rejecting the null indicates the linear fit is poor and suggests we are near a maximum (or ridge, or saddle point) of the response surface.

9.3 Second-order response surface designs

Second-order response surface designs try to apply Newton’s method to optimize a function $f$ whose gradient $\nabla f(x)$ and Hessian $\nabla^2 f(x)$ can only be approximated by experiment.

We will need the Hessian, so following the same Taylor expansion argument, we will need to include the second-order term (hence the name): \[ f(x) \approx f(x^*) + \nabla f(x^*)\T (x - x^*) + \frac{1}{2} (x - x^*)\T \nabla^2 f(x^*) (x - x^*). \] This approximates $f(x)$ as a quadratic function of $x$, so we will fit a model with quadratic terms. For instance, if there are two predictors, $X_1$ and $X_2$, we will fit the model \[ Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \beta_3 X_1^2 + \beta_4 X_2^2 + \beta_5 X_1 X_2 + \epsilon. \] If we fit this model and take its second derivatives to estimate $\nabla^2 f(x)$, we will find the estimated Hessian depends on $\beta_3$, $\beta_4$, and $\beta_5$ (see Exercise 9.1), so it is crucial that we estimate these well.

The standard first-order designs of Section 9.2 will not work here, as they do not allow us to fit quadratic terms. We will need additional design points.

We hence want a design that

Gives us the best possible estimate of both $\nabla f(x)$ and $\nabla^2 f(x)$
Lets us estimate $\hat \sigma^2$, so we can tell if the quadratic approximation fits well
Is, ideally, orthogonal, so the variance of slope and Hessian estimates is as small as possible (and uncorrelated).

9.3.1 Central composite designs

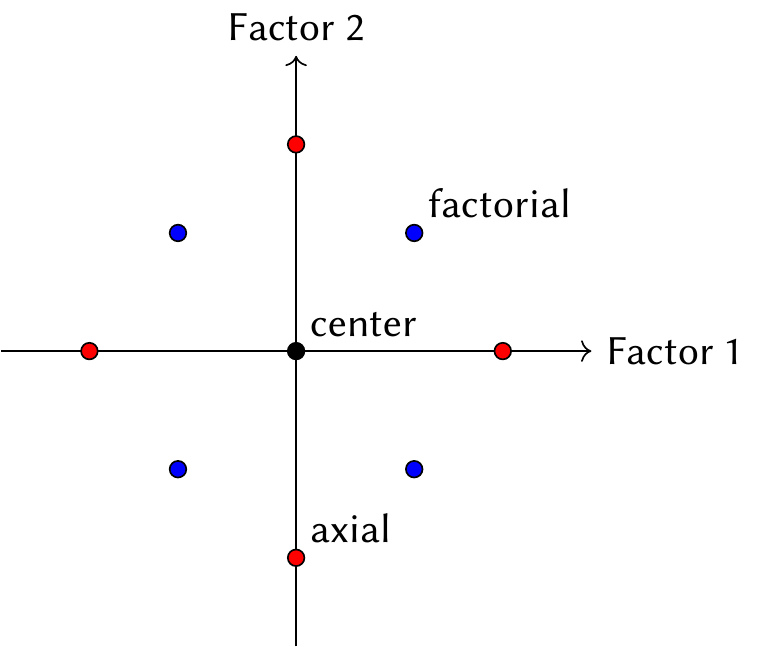
The typical solution to these requirements is the central composite design. A central composite design starts with a standard first-order design with $n_0$ center points and $n_f$ factorial points. It then adds $n_a$ axial points, which are at values $\pm \alpha$ of each treatment factor, as illustrated in Figure 9.1.

Figure 9.1: A central composite design with two treatment factors, based on a $2^2$ full factorial. There is one center point (in black), four factorial points (blue), and four axial points (red), drawn here with $\alpha = 1.75$.

As before, we typically choose $n_0$ between 3 and 6 to ensure $\hat \sigma^2$ can be estimated. Choosing $\alpha$ is slightly more difficult, and depends on the specific design properties we want. One desirable property could be that the variance of $\hat f(X)$ is the same in any direction.

Definition 9.3 (Rotatable designs) An experimental design is rotatable if $\var(\hat f(x))$, the variance of the fitted model’s prediction at a point $x$, is a function only of the distance $\|x\|_2^2$ of the point to the origin.

Hence in a rotatable design the variance is symmetric around the origin. This is a reasonable request: unless one factor is more important than the others, we should choose a design that obtains equal information about the response surface in each direction. We can obtain a rotatable central composite design by carefully choosing $\alpha$.

Theorem 9.1 (Rotatable central composite designs) A central composite design is rotatable if $\alpha = n_f^{1/4}$, where $n_f$ is the number of factorial points.

Proof. See Box and Hunter (1957).

We can also ask for the design to be orthogonal, i.e., the columns in the design matrix are all orthogonal to each other (except for the intercept). But here it is less obvious why this is desirable. Why should the design matrix columns for $X_1$ and $X_1^2$ be orthogonal to each other? Ensuring they are orthogonal to the $X_2$ and $X_2^2$ columns is reasonable, so the effect estimates are uncorrelated, but requiring all pairs of columns to be orthogonal is less obviously useful.

Nonetheless, it’s convenient if you are conducting tests for specific coefficients, for instance if you want to test if a quadratic relationship is truly necessary for one specific treatment factor. It also simplifies computation, of course, by reducing the multiple regression problem to separate univariate regression problems, but this is not a concern if we’re using a computer to fit our models.

The requirements on $\alpha$ and $n_0$ for orthogonality are more complicated than for rotatability; see Dean, Voss, and Draguljić (2017), section 16.4.2. It may not always be possible for a design to be both orthogonal and rotatable.

9.3.2 Fitting the quadratic model

Once we have constructed a central composite design and collected the data, we can fit a second-order polynomial model. Rather than writing out sums of linear, quadratic, and interaction terms, it is easier to consider the model in matrix form. Let $X \in \R^p$ be a point in the design space. Then a quadratic model for the response can be written as \[ Y = f(X) = \beta_0 + \beta\T X + X\T B X + \epsilon, \] where $\beta_0$ is the intercept, $\beta \in \R^p$ is a vector of slope coefficients, and $B$ is a $p \times p$ matrix. The diagonal entries of $B$ give the coefficients of quadratic terms, while the off-diagonal entries are the coefficients of interactions between pairs of variables. This model can be fit using least squares in the usual way, as you have likely done before for many models with polynomials and interactions, and the coefficients rewritten in this matrix and vector form.

A quadratic equation has a stationary point that is either a minimum, maximum, or saddle point. We can find the stationary point $x_s$ by setting the gradient to zero: \[\begin{align*} 0 &= \nabla f(x_s) \\ &= \beta + 2 B x_s \\ x_s &= - \frac{1}{2} B^{-1} \beta. \end{align*}\] To determine if this is a minimum, maximum, or saddle point, we must examine the second derivatives. When you learned quadratic equations in one variable, you learned to use the sign of the second derivative to check. Here there is an entire matrix of second derivatives, the Hessian: \[ \nabla^2 f(x) = 2 B. \] This is the same Hessian as a quadratic model that omits the linear terms, and the Hessian is the same regardless of $x$. For simplicity, then, consider the purely quadratic model \[ f^*(X) = X\T B X. \] Calculate the eigenvalue decomposition $B = UDU^{-1}$, where $U$ is the matrix of eigenvectors and $D$ a diagonal matrix of eigenvalues. Since $B$ is symmetric, $U$ is orthogonal and $U^{-1} = U\T$. Then \[\begin{align*} f^*(X) &= X\T UDU^{-1} X\\ &= (U\T X)\T D (U\T X) \\ &= \sum_{j=1}^p \lambda_j (U\T X)_j^2, \end{align*}\] where $\lambda_1, \dots, \lambda_p$ are the eigenvalues of $B$. When each eigenvalue $\lambda_j > 0$, this function must be nonnegative regardless of $X$; when each eigenvalue $\lambda_j < 0$, this function must be nonpositive regardless of $X$; and when the eigenvalues have mixed signs, the sign depends on the particular $X$. The stationary point of this quadratic is at $U\T X = 0$, at which point it has value 0. Hence when the eigenvalues are all positive, the stationary point must be the minimum; when they’re negative, it must be the maximum, and when they’re mixed signs, it is a saddle point.

Again, this translates back to our actual quadratic function $f(X)$, because adding the intercept and linear terms does not change whether a point is a minimum, maximum, or saddle point. Examining the eigenvalues of $B$ (and hence of the Hessian) is the exact equivalent of examining the sign of the second derivative in one dimension. This check is known in response surface design as canonical analysis.

We can use canonical analysis to determine whether we have found a maximum and where the maximizer is.

9.4 The response-surface process

Based on the above considerations, we can write the general process for finding the value $x^*$ that maximizes an unknown function $f(X)$ through repeated experiments. It looks something like this:

Select a reasonable starting point $x^{(0)}$ for all factors.
Select a first-order response surface design around this point, such as a standard first-order design. Conduct the experiment.
Fit a linear model to the first-order design and test its fit. If it fits reasonably well, find the direction of steepest ascent, take a step in that direction, and return to step 2. Otherwise, continue to step 4.
Run a second-order response surface design. Fit the quadratic model and use canonical analysis to determine if you are near a maximum. If you are near a maximum, declare the stationary point to be your desired $x^*$, or perhaps run one more experiment there to verify the exact value. If you are near a minimum or saddle point, figure out how to move to get away from it, and return to step 2.

Fortunately, packages exist to calculate common designs, the models to be fit are standard linear and quadratic regression models, and canonical analysis can be done easily by many packages. Let’s examine examples using one such package, the rsm package for R.

Example 9.1 (Generating designs with rsm) The rsm package can generate common response surface designs. Its ccd() function generates central composite designs, from which we can extract the factorial design and center points (if desired) and the axial points needed for a second-order design.

For example, say we have 2 factors named A and B, and want a design with 4 center points and $\alpha = 1.4$:

library(rsm)

ccd(~ A + B, n0 = 4, alpha = 1.4)

   run.order std.order A.as.is B.as.is Block
1          1         3    -1.0     1.0     1
2          2         4     1.0     1.0     1
3          3         8     0.0     0.0     1
4          4         2     1.0    -1.0     1
5          5         5     0.0     0.0     1
6          6         1    -1.0    -1.0     1
7          7         7     0.0     0.0     1
8          8         6     0.0     0.0     1
9          1         4     0.0     1.4     2
10         2         1    -1.4     0.0     2
11         3         8     0.0     0.0     2
12         4         3     0.0    -1.4     2
13         5         2     1.4     0.0     2
14         6         5     0.0     0.0     2
15         7         6     0.0     0.0     2
16         8         7     0.0     0.0     2

Data are stored in coded form using these coding formulas ...
A ~ A.as.is
B ~ B.as.is

The design data frame is generated in a random order (so you run the experiment in random order and avoid any systematic time/order biases), though you can use the std.order column to sort. The Block column splits the runs into blocks; here, one block is the factorial design and one block gives the axial points. Notice there are 4 center points for the factorial and 4 additional center points for the second-order axial design.

The cube() function generates only the first-order points for a standard first-order design. It also supports fractional factorials. We can specify a defining relation; for example, if our defining relation is $I = ABC$, we can generate a half-fraction:

cube(~ A + B + C, blockgen = ~ A * B * C, n0 = 5)

  run.order std.order A.as.is B.as.is C.as.is
1         1         2       1       1      -1
2         2         1      -1      -1      -1
3         3         3       1      -1       1
4         4         5       0       0       0
5         5         6       0       0       0
6         6         8       0       0       0
7         7         7       0       0       0
8         8         4      -1       1       1
9         9         9       0       0       0

Data are stored in coded form using these coding formulas ...
A ~ A.as.is
B ~ B.as.is
C ~ C.as.is

Example 9.2 (Fitting a model with rsm) The rsm package provides a sample dataset from a chemical experiment. A process was run at different temperatures for different times, and the yield of the chemical measured as the response. The ChemReact1 data frame has factorial and center points of the experiment:

library(rsm)
ChemReact1

  Time Temp Yield
1   80  170  80.5
2   80  180  81.5
3   90  170  82.0
4   90  180  83.5
5   85  175  83.9
6   85  175  84.3
7   85  175  84.0

We can see the different time and temperature settings. To analyze a response surface model, it’s good to first “code” the data by rescaling the treatments to the range $\pm 1$; we can do this with the coded.data() function:

coded_cr1 <- coded.data(ChemReact1,
                        time ~ (Time - 85) / 5,
                        temp ~ (Temp - 175) / 5)

The coding scheme is stored in coded_cr1 so it can be used later.

Now we use the rsm() function to fit the response surface model. Of course, we could simply use lm() with the appropriate terms, but rsm() adds a few features to make it easier to fit and interpret standard response surface models. For example, the FO() term in the model formula specifies a first-order linear model:

cr1_fit <- rsm(Yield ~ FO(time, temp), data = coded_cr1)

summary(cr1_fit)


Call:
rsm(formula = Yield ~ FO(time, temp), data = coded_cr1)

            Estimate Std. Error  t value  Pr(>|t|)    
(Intercept) 82.81429    0.54719 151.3456 1.143e-08 ***
time         0.87500    0.72386   1.2088    0.2933    
temp         0.62500    0.72386   0.8634    0.4366    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Multiple R-squared:  0.3555,    Adjusted R-squared:  0.0333 
F-statistic: 1.103 on 2 and 4 DF,  p-value: 0.4153

Analysis of Variance Table

Response: Yield
               Df Sum Sq Mean Sq F value  Pr(>F)
FO(time, temp)  2 4.6250  2.3125  1.1033 0.41534
Residuals       4 8.3836  2.0959                
Lack of fit     2 8.2969  4.1485 95.7335 0.01034
Pure error      2 0.0867  0.0433                

Direction of steepest ascent (at radius 1):
     time      temp 
0.8137335 0.5812382 

Corresponding increment in original units:
    Time     Temp 
4.068667 2.906191

The summary includes the ANOVA table and the direction of steepest ascent. We could move in this direction, but the “Lack of fit” row of the ANOVA table (which gives the $F$ test described in Section 9.2.3) suggests there is quadratic curvature here and we need to use a second-order model.

The ChemReact data frame contains the same observations, plus additional points to form a central composite design. The central composite points were collected as a separate block. Let’s code it and fit a second-order model using a SO() term.

coded_cr <- coded.data(ChemReact,
                       time ~ (Time - 85) / 5,
                       temp ~ (Temp - 175) / 5)

cr_fit <- rsm(Yield ~ Block + SO(time, temp), data = coded_cr)

summary(cr_fit)


Call:
rsm(formula = Yield ~ Block + SO(time, temp), data = coded_cr)

             Estimate Std. Error  t value  Pr(>|t|)    
(Intercept) 84.095427   0.079631 1056.067 < 2.2e-16 ***
BlockB2     -4.457530   0.087226  -51.103 2.877e-10 ***
time         0.932541   0.057699   16.162 8.444e-07 ***
temp         0.577712   0.057699   10.012 2.122e-05 ***
time:temp    0.125000   0.081592    1.532    0.1694    
time^2      -1.308555   0.060064  -21.786 1.083e-07 ***
temp^2      -0.933442   0.060064  -15.541 1.104e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Multiple R-squared:  0.9981,    Adjusted R-squared:  0.9964 
F-statistic: 607.2 on 6 and 7 DF,  p-value: 3.811e-09

Analysis of Variance Table

Response: Yield
                Df Sum Sq Mean Sq   F value    Pr(>F)
Block            1 69.531  69.531 2611.0950 2.879e-10
FO(time, temp)   2  9.626   4.813  180.7341 9.450e-07
TWI(time, temp)  1  0.063   0.063    2.3470    0.1694
PQ(time, temp)   2 17.791   8.896  334.0539 1.135e-07
Residuals        7  0.186   0.027                    
Lack of fit      3  0.053   0.018    0.5307    0.6851
Pure error       4  0.133   0.033                    

Stationary point of response surface:
     time      temp 
0.3722954 0.3343802 

Stationary point in original units:
     Time      Temp 
 86.86148 176.67190 

Eigenanalysis:
eigen() decomposition
$values
[1] -0.9233027 -1.3186949

$vectors
           [,1]       [,2]
time -0.1601375 -0.9870947
temp -0.9870947  0.1601375

The summary includes the canonical analysis of this fit, including the stationary point and the eigenvalues of the Hessian. Here they are both negative, indicating we have indeed found a maximum and not just a stationary point.

9.5 Exercises

Exercise 9.1 (Hessian of the polynomial model) Consider fitting the polynomial model \[ Y = f(X) + \epsilon = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \beta_3 X_1^2 + \beta_4 X_2^2 + \beta_5 X_1 X_2 + \epsilon. \] Calculate $\nabla^2 f(x)$. Show that it depends only on $\beta_3$, $\beta_4$, and $\beta_5$.

Exercise 9.2 (Quadratic fits to standard first-order designs) In Section 9.2.2, we suggested that regardless of the number of center-point replicates, it’s not possible to fit a full quadratic model to a standard first-order design. We showed this is true when there are $p = 2$ treatment factors, because there are 5 design points but 6 parameters to estimate.

Derive an expression for the number of parameters in a quadratic fit to $p$ parameters, including all interactions. Compare this to the number of design points in a full factorial first-order design.
Show that for any $p > 1$, the quadratic fit is not uniquely identified.

Hint: Show there are more parameters than design points for a simple base case, such as $p = 3$. Then show that when $p$ increases by 1, the number of parameters must grow faster than the number of design points.

Exercise 9.3 (Orthogonal first-order designs) In Section 9.2, we stated that a desirable property of a first-order design is that it minimizes the average variance of the regression coefficients, \[ \frac{1}{p + 1} \trace(\var(\hat \beta)). \] Consider the case where we center and scale the design matrix, so that (apart from the intercept) each column of $\X$ has mean 0 and sample variance 1, and we assume constant error variance.

The centering and scaling imply constraints on the sums of columns of $\X$. Write these constraints in terms of the individual entries $x_{ij}$ of the design matrix.
Rewrite the minimization in terms of $(\X\T \X)^{-1}$, so it can be connected to the design matrix $\X$.
Use the eigenvalue decomposition to show that because $\X\T\X$ is symmetric and positive definite, the trace of $(\X\T\X)^{-1}$ trace can be written in terms of the eigenvalues of $\X\T\X$. Use the eigenvalues to connect this to the trace of $\X\T\X$.
Using the constraints you found in part 1, show that $\trace(\X\T\X)$ must be equal to $n + p(n - 1)$.
TODO Further steps to show that minimizing the average variance implies that the columns of $\X$ must be orthonormal.

Exercise 9.4 (Quadratic fits without center points) Argue that in the standard first-order design (Section 9.2.2), omitting the center point makes it impossible to test for lack of fit using quadratic terms. TODO

Exercise 9.5 (The CHICK experiment) Pollock, Ross-Parker, and Mead (1979) created the CHICK game, an experimental design problem where the player must figure out how to optimize the response. The situation is based on actual research and the setup of a University Poultry Research Farm.

Consider an experiment on baby chicks being grown in a henhouse. They may be fed diets based on either wheat or maize (corn). We would like to figure out how much copper should be added to either diet to improve their rate of growth:

We know that 150 units of copper added to either diet seems to improve growth. We are also fairly certain that there is a level of copper beyond which toxic effects will reduce growth rate. It seems clear, then, that there is a best quantity of copper to add to maximize growth rate, but this may well be different for wheat and maize diets.

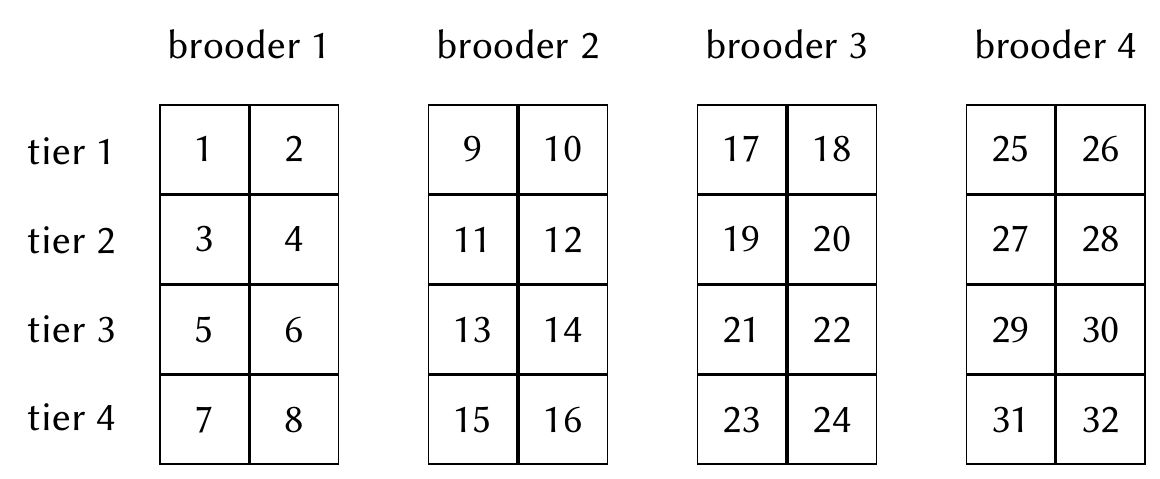
The chicks are grown in cages arranged in a henhouse. There are 32 cages, each of which contains 16 chicks. Groups of 8 cages are stacked into “brooders”, each of which consists of cages in four vertical tiers, as shown in Figure 9.2. The experimenters expect there is a brooder effect, “presumably attributable to the position of brooders within the hen house”, as well as a tier effect. As the chicks in each cage share their food supply, the diet (wheat or maize, and the amount of copper) must be assigned to entire cages. The response is the average growth of the chicks in each cage over the course of the experiment, measured by their increase in weight from the beginning to the end of the experiment.

Figure 9.2: Physical arrangement of the 32 CHICK cages into 4 brooders, each having 4 tiers of cages.

The goal is to design a series of experiments (up to 5) that can be used to find the optimum amount of copper to add to wheat and maize diets, keeping in mind the amount may be different depending on the diet.

Describe the experiment precisely: How many treatments are there? What are their levels? How many blocking variables are there and how many values do they have?
To conduct a first-order response surface design, describe the treatment combinations you would like to use. How many are necessary?

Hint: If you are willing to give up your center points, you may find a particularly good design option in the next step.
Based on the number of blocking variables, the number of treatments you’d like to evaluate, and the experimental setup, design your first experiment. Allocate treatment to each cage. Show your allocations and describe how you arrived at them: what kind of design is this, and how did you choose it?
The file chick-experiment.R contains code to simulate the results of your experiment. Download the file and load it into your R session using source(). The simulate_chick() function accepts a data frame specifying your experimental design. This should have 32 rows, one per cage, and columns indicating the tier, brooder, diet, and copper level for each cage. See the comment at the top of the file for details.

Construct your data frame matching your design in part 3. Call simulate_chick() to obtain the response. Analyze the results. Decide on a new values of copper to try in the next experiment and list the values you will try.

Exercise 9.6 (Ammoniation yield) Chang, Kononenko, and Franklin (1960) were interested in optimizing the production of 2,5-dimethylpiperazine (DMP), which is made by ammoniating 1,2-propanediol in a reaction chamber. Ammonia and 1,2-propanediol are put into the chamber with a catalyst and hydrogen gas, and the chamber is then heated to a specified temperature for 4 hours. They considered four treatment factors, here listed with the values they coded as $\pm 1$:

Ammonia quantity (51 to 153 grams)
Maximum temperature (230 to 270 C)
Water quantity (100 to 500 grams)
Initial hydrogen pressure (500 to 1,200 psi)

The response is the percent yield of DMP. They decided to conduct a response surface experiment. The data is contained in ammoniation.csv. Rows 1-17 give an initial first-order design, while the remaining rows give the extra points needed for a second-order design. Note that row 17 is the average of six trials; the individual results were not reported separately.

Review the data. What type of design was used for the first-order experiment? What type of design was used for the second-order experiment?
Analyze the first-order experiment data (rows 1-17). Fit a first-order model and report the direction of steepest ascent. (You do not need to account for row 17 being an average, but this does prevent you from conducting a test for linearity.)
Add the remaining rows and fit a second-order quadratic model. Use canonical analysis to report the stationary point and determine whether it is an optimum.

(Wu and Hamada 2021, exercise 10.10)

This intuition appears to be common in response surface designs, but I’m not sure it’s justified by an appeal to functions having particular smoothness and curvature properties. Perhaps experimental design theorists just expect that in nature, response surfaces will be nice well-behaved functions, and that no physical response surface could look like the Weierstrass function.↩︎