23 Mixed and Hierarchical Models

In the linear and generalized linear models so far, the regression parameters ($\beta$) are fixed properties of the population, and our task is to estimate them with as much precision as possible. We then interpret the parameters to make statements about the population. The parameters are fixed, so their effects are known as fixed effects.

But it is possible for the relationship between predictor and response to also depend on random quantities—on properties of the particular random sample we obtain. When this happens, some of the model parameters are random, and so their effects are known as random effects.

We can construct linear and generalized linear models with random effects, known as random effects models or mixed effects models (“mixed” because they contain both fixed and random effects). As we will see, these are useful for modeling many kinds of data with grouped or repeated structure. They can also be thought of as a way of applying penalization, as discussed in Chapter 19, to regression coefficients in a more structured way, and so can give useful estimates even when the parameters are not truly random.

23.1 Motivating examples

Many regression problems involve data that comes from a random sample from a population (or that we at least treat as a random sample). But we are concerned with problems where the effects are random. Consider some examples.

Example 23.1 (Small area estimation) A social scientist is constructing a map of poverty across the United States as part of a project to suggest government policies that might help low-income areas. The scientist wants to estimate the average income of individuals in every county in the US, and pays a polling company to conduct a large, representative national survey. Survey respondents indicate their county of residence and their income.

Each observation is one person, but we want to estimate county averages, so it is reasonable to model respondent $i$’s income as \[ \text{income}_i = \alpha_{\text{county}[i]} + e_i, \] where $\text{county}[i]$ represents the number of the county respondent $i$ lives in. As there are about 3,200 counties, there are about 3,200 values of $\alpha$, and their estimates $\hat \alpha$ give us the average income per county. We can treat $\alpha$ as a fixed unknown parameter, making this a simple regression or ANOVA problem; or we can imagine the counties as a sample from the process generating county incomes every year, making them random effects. As we will see, this has some advantages.

This is an example of a small area estimation problem, in which the goal is to make inferences about individual geographic areas from survey or sample data. The data is hierarchical: the units are survey respondents, who are grouped within counties, which are all within the United States.

Example 23.2 (Sleep deprivation) Belenky et al. (2003) conducted an experiment to measure the effect of sleep deprivation on reaction time. A group of 18 experimental subjects spent 14 days in the laboratory. For the first 3 nights, they were required to be in bed for eight hours per night; for the next seven days, they were only allowed three hours per night. Each day, they completed several tests of alertness and reaction time, including one that directly measured how quickly they pressed a button after seeing a visual stimulus. Our data hence includes 10 observations per subject: three days of baseline measurements and seven days of sleep deprivation.

The goal is to measure the effect of sleep deprivation on reaction time, including how reaction time changes as the number of days of deprivation increases. We might model respondent $i$’s reaction time as \[ \text{time}_i = \beta_0 + \beta_1 \text{days} + e, \] but it is reasonable to expect that each subject had a different reaction time at baseline (0 days) and that each was affected differently by sleep deprivation. Instead we might allow both the slope and intercept to vary by subject: \[ \text{time}_i = \alpha_i + \beta_i \text{days} + e. \] Here $\alpha$ and $\beta$ are both random effects.

23.2 Mixed models

A mixed model dramatically reduces the number of parameters to estimate by adding some structure to the regression problem.

Definition 23.1 (Mixed model) A mixed model is a linear model written as \[ Y_i = \underbrace{\beta\T X_i}_{\text{fixed effects}} + \underbrace{\gamma\T Z_i}_{\text{random effects}} + e_i, \] where $\beta \in \R^p$ is a fixed population parameter, $X_i \in \R^p$ is a vector of known covariates, $\gamma \in \R^q$ is a vector of random effects, and $Z_i \in \R^q$ is another vector of known covariates. Crucially, $\gamma$ is a random variable that is assumed to be drawn from a particular distribution. One can also write the model in matrix form as \[ \Y = \beta\T \X + \gamma\T \Z + e. \]

Generally it is assumed that $\E[e] = 0$, $\cov(\gamma, e) = 0$, and the distribution of $\gamma$ is a parametric family with mean 0 and known or estimable covariance.

Transforming a particular model into a mixed model simply requires translating its features into columns of $X$ and $Z$, just as we did with ordinary linear models in Chapter 7.

Example 23.3 (Random intercepts model) In the small area estimation example (Example 23.1), let $X$ contain an intercept column and let $Z$ contain an indicator of county (including columns for every county, so none is absorbed in the intercept). Then let \[ \gamma \sim \normal(\zerovec, \sigma_\gamma^2 I). \] Now the model is \[ \text{income} = \beta_0 + \gamma\T \Z + e, \] $\beta_0$ represents the overall mean across counties (because $\gamma$ has mean zero) and the entries of $\gamma$ give the difference between each county’s mean and the grand mean. We need only estimate two parameters, $\beta_0$ and $\sigma_\gamma^2$, despite there being over 3,200 individual counties.

Example 23.4 (Random slopes model) In the sleep deprivation study (Example 23.2), let $X$ contain an intercept column and the number of days of sleep deprivation, so $\beta \in \R^2$. Then let $Z$ contain an indicator of subject (and hence a column for every subject) as well as columns for the interaction of subject and days. We can hence partition the random effects part of the model: \[ \gamma\T \Z = \begin{pmatrix} \gamma_1 \\ \vdots \\ \gamma_{18} \\ \gamma_{19} \\ \vdots \\ \gamma_{36} \end{pmatrix}\T \left(\begin{array}{cccc|cccc} 1 & 0 & \cdots & 0 & 0 & 0 & \cdots & 0\\ 1 & 0 & \cdots & 0 & 1 & 0 & \cdots & 0\\ \vdots & & & & & & & \vdots \\ 0 & 0 & \cdots & 1 & 0 & 0 & \cdots & 8\\ 0 & 0 & \cdots & 1 & 0 & 0 & \cdots & 9 \end{array}\right). \] Here the first 18 entries of $\gamma$ correspond to random intercepts for each of the 18 subjects, while the next 18 entries are random interactions for each subject. We then assemble them into the model \[ \text{time} = \beta_0 + \beta_1 \text{days} + \gamma\T \Z + e. \] The interaction allows the intercept and slope of the relationship to be random effects, not fixed, with the mean intercept and slope estimated by $\beta_0$ and $\beta_1$. For example, for subject 1 on day $d$, $Z = (1, 0, \dots, 0, d, 0, \dots, 0)\T$, and so the model is \[\begin{align*} \text{time} &= \beta_0 + \beta_1 \text{days} + \gamma_1 + \gamma_{19} \text{days} + e\\ &= (\beta_0 + \gamma_1) + (\beta_1 + \gamma_{19}) \text{days} + e. \end{align*}\]

With this setup, it’s not reasonable to say that the entries of $\gamma$ are simply iid with common variance $\sigma_\gamma^2$. The intercept and interaction effects may have different variances, and the effects for subject $i$ are likely correlated with each other, just as the slope and intercept are correlated in an ordinary linear model. A reasonable choice might instead be that $\gamma \sim \normal(\zerovec, \Sigma)$, where \[ \Sigma_{ij} = \begin{cases} \sigma_0^2 & \text{if $i = j$ and $i \leq 18$}\\ \sigma_1^2 & \text{if $i = j$ and $i > 18$}\\ \sigma_{01} & \text{if $|i - j| = 18$}\\ 0 & \text{otherwise.} \end{cases} \] Hence the intercepts have variance $\sigma_0^2$, the interaction slopes have variance $\sigma_1^2$, and the slope and intercept for one subject have correlation $\sigma_{01}$, but subjects are not correlated with each other.

In each case we have written the model to make the mean of the random effects zero, so their mean is estimated as a fixed effect. This is convenient because the software we use for estimation defaults to setting the mean of all random effects to zero.

23.3 Estimating mixed models

Estimating the parameters of a mixed model is more complicated than in ordinary linear regression. Only in simple cases can we reduce the problem to simple sums of squares; more complex covariance structure, such as in Example 23.4, means standard least-squares geometry does not apply. We have to estimate multiple variance parameters. The typical approach is to assume a distribution for the errors $e$ so that we can use maximum likelihood.

23.3.1 The likelihood

We can write a mixed model with normal errors in vector form as \[\begin{align*} \Y \mid \gamma &\sim \normal(\beta\T \X + \gamma\T \Z, \sigma^2 I)\\ \gamma &\sim \normal(\zerovec, \Sigma), \end{align*}\] where $\Sigma$ is a covariance matrix giving the covariance of the random effects. We use bold letters $\Y$, $\X$, and $\Z$ to denote the complete vectors and matrices of $n$ observations.

The covariance matrix $\Sigma$ is often structured, as we saw in Example 23.4. As we assume $\cov(\gamma, e) = 0$, we can also write this marginally as \[ \Y \sim \normal(\beta\T \X + \gamma\T \Z, \sigma^2 I + \Z \Sigma \Z\T). \] Hence the likelihood of $\Y$ can be written using the normal density in terms of $\beta$, $\gamma$, $\sigma^2$, and $\Sigma$. The matrix $\Sigma$ has $q^2$ entries, making it difficult to estimate in general, but when it is structured there may only be a few parameters to estimate.

Example 23.5 (Likelihood of the random intercepts model) The random intercepts model of Example 23.3 can be written as \[\begin{align*} \Y \mid \gamma &\sim \normal(\beta\T \X + \gamma\T \Z, \sigma^2 I)\\ \gamma &\sim \normal(\zerovec, \sigma^2_\gamma I), \end{align*}\] replacing the general covariance matrix $\Sigma$ with a single parameter $\sigma_\gamma^2$, because the random intercepts for different teachers are assumed to be independent. We can write this marginally as \[ \Y \sim \normal(\beta\T \X + \gamma\T \Z, (\sigma^2 + \sigma_\gamma^2) I), \] because each row of $\Z$ contains only one nonzero entry (1), so $\Z\Sigma\Z\T$ when $\Sigma = \sigma_\gamma^2 I$ reduces to $\sigma_\gamma^2 I$.

The likelihood is then the product of normal densities, as in any normal likelihood.

23.3.2 Maximum likelihood and optimization

In principle, maximum likelihood estimation is straightforward and just requires us to maximize with respect to $\beta$, $\gamma$, $\sigma^2$, and $\Sigma$. In practice, however, maximum likelihood estimation is difficult here. The $q \times q$ covariance matrix $\Sigma$ has $q^2$ parameters to estimate, and it is constrained, since covariance matrices must be positive definite; the MLE can occur on a boundary of the space, making many optimizers unhappy. Special cases, such as the random intercepts model in Example 23.5, can be straightforward, but other cases require clever optimization.

But the problem is not just optimization. The maximum likelihood estimates of the variance are biased. This is true even in ordinary linear regression: Theorem 5.2 showed that the unbiased estimator of $\sigma^2 = \var(e)$ in a simple linear regression model is \[ S^2 = \frac{\RSS(\hat \beta)}{n - p}, \] where $p$ is the number of regressors and $\RSS(\hat \beta)$ is the residual sum of squares. But the maximum likelihood estimate is \[ \hat \sigma^2_\text{MLE} = \frac{\RSS(\hat \beta)}{n}. \]

This is a critical problem in many mixed model applications, as we often interpret the variance components: the proportion of variance from $\var(e)$ versus from the random effects. This is a natural way to measure the “size” of the random effects, but if the variance estimates are all biased, variance component estimates will all be biased.

Worse, in some mixed model settings the number of parameters grows with $n$. For example, if we have a fixed effect for a factor variable, and the number of levels of that factor grows with $n$, the number of fixed effect parameters will grow with $n$. In this case, the MLE is inconsistent: as $n \to \infty$, the MLE does not converge to the true parameter values. This is called the Neyman–Scott problem.

The solution is restricted maximum likelihood estimation, known as REML. TODO

23.3.3 Obtaining random effects estimates

Maximizing the likelihood of a mixed effects model gives us values for $\hat \beta$, $\hat \sigma^2$, and $\hat \Sigma$. But $\gamma$ is a random variable, not a parameter, so we do not get estimates of the random effects! We may still want reasonable values for them, so we will have to be creative.

We can imagine a Bayesian setup for $\gamma$. We have a prior distribution $p(\gamma)$ specified in our mixed model ($\normal(\zerovec, \Sigma)$) and we have a likelihood $p(y \mid \gamma)$, treating all other parameters as fixed. We can use Bayes’ theorem to obtain the posterior $p(\gamma \mid y)$. Because the likelihood and prior are both normal, the posterior is also normal, making it straightforward to derive the posterior mean.

Exercise 23.1 (Posterior mean random intercepts) In the random intercepts model of Example 23.5, the posterior mean of $\gamma$ can be derived simply. By Bayes’ theorem, \[ p(\gamma \mid y) \propto p(y \mid \gamma) p(\gamma), \] and both the prior and likelihood are Gaussian. If we multiply the likelihoods, ignoring the constant factors, we obtain \[\begin{align*} p(\gamma \mid y) &\propto \exp\left( -\frac{\|\Y - \X\beta - Z \gamma\|_2^2}{2 \sigma^2} \right) \exp\left( - \frac{\|\gamma\|_2^2}{2 \sigma_\gamma^2} \right) \end{align*}\] TODO

(In principle, a Bayesian setup should put priors on all the parameters. Here we just fix them at their MLE estimates. This is “empirical Bayes”.)

23.3.4 Making predictions

TODO

23.3.5 Fitting in R

In R, the lme4 package is the most popular package for fitting mixed models (Bates et al. 2015). Its lmer() function supports a variety of mixed-effects models, and its glmer() function does the same for GLMs.

To indicate fixed or random effects, lme4 uses a special formula syntax. It follows R’s usual conventions (Section 6.2): a formula of the form y ~ x1 + x2 specifies y as the response variable plus x1 and x2 as fixed effects. But the | character has special meaning. The right-hand side of the formula can contain terms of the form (expression | group). The expression can be multiple terms, interpreted just like in any model formula; the group is a factor variable, and says the terms in the expression are random effects that vary by group. For example:

(1 | factor): A random intercept term. The intercept varies by level of the factor.
(1 + x | factor): A random intercept and slope. Both the slope of x and its intercept vary by level of the factor, and the slope and intercept may be correlated with each other.

The lmer() and glmer() functions use this syntax to construct the random effect matrix $Z$. Let’s see an example.

Example 23.6 (Simulated random intercepts) Let’s simulate data from the small area estimation example (Example 23.1). For simplicity, we’ll model 26 counties, labeled A through Z. Each row of data is one survey respondent, who lives in one county. Each county has a different mean income. We’ll transform income to be normally distributed to make things easier.

library(regressinator)
library(gtools) # for rdirichlet

county_effects <- sapply(c(LETTERS, letters), function(l) rnorm(1, sd = 0.25))
county_props <- as.vector(rdirichlet(1, rep(2, length(county_effects))))

respondent_pop <- population(
  county = predictor(rfactor, levels = c(LETTERS, letters),
                     prob = county_props),
  income = response(
    1 + by_level(county, county_effects),
    error_scale = 0.5
  )
)

respondents <- respondent_pop |>
  sample_x(n = 1000) |>
  sample_y()

We’ll model an intercept and a random effect for county. Here’s the mixed-effect model fit:

library(lme4)

survey_fit <- lmer(income ~ (1 | county),
                    data = respondents)
summary(survey_fit)

Linear mixed model fit by REML ['lmerMod']
Formula: income ~ (1 | county)
   Data: respondents

REML criterion at convergence: 1596.6

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-3.5139 -0.6747 -0.0155  0.6670  3.6467 

Random effects:
 Groups   Name        Variance Std.Dev.
 county   (Intercept) 0.04891  0.2212  
 Residual             0.26816  0.5178  
Number of obs: 1000, groups:  county, 52

Fixed effects:
            Estimate Std. Error t value
(Intercept)  0.99218    0.03642   27.24

TODO interpret each part of the summary table

The ranef() function extracts the posterior mean random effects:

ranef(survey_fit)

$county
    (Intercept)
A -0.0786252993
B -0.0113137362
C -0.1590036894
D -0.0491362222
E  0.4758944640
F  0.0940416960
G  0.0661769644
H  0.1225221821
I  0.0329334458
J  0.1056344677
K  0.2471586891
L  0.2787006500
M -0.1296345668
N  0.1156792426
O -0.2524576152
P -0.2740940409
Q  0.0087332239
R -0.0312313029
S  0.0213195123
T -0.0622115362
U -0.1104198152
V -0.1076640105
W  0.1959719870
X  0.0698524488
Y  0.0004194173
Z -0.1876976644
a  0.2730339082
b -0.2813864002
c  0.1662499337
d -0.3241821283
e  0.1222395302
f  0.1148958674
g  0.0006623908
h -0.2689754790
i  0.0403812403
j  0.1400119931
k  0.0745620037
l -0.0350879289
m  0.2042235816
n  0.3007470446
o -0.1695605242
p -0.1236798057
q  0.0025377745
r  0.0530964437
s  0.0172706926
t -0.2239913258
u -0.0154584430
v  0.3938633990
w -0.4057198672
x -0.0287322671
y -0.1735483292
z -0.2350021965

with conditional variances for "county"

library(ggplot2)

data.frame(true = county_effects,
           ranefs = ranef(survey_fit)$county[["(Intercept)"]]) |>
  ggplot(aes(x = county_effects, y = ranefs)) +
  geom_point() +
  geom_abline(intercept = 0, slope = 1, linetype = "dashed") +
  geom_smooth(method = "lm")

library(dplyr)
library(broom)

tidy(lm(income ~ county, data = respondents)) |>
  filter(term != "(Intercept)") |>
  arrange(desc(estimate)) |>
  mutate(rownum = 1:n()) |>
  ggplot(aes(x = std.error, y = estimate, ymin = estimate - 2 * std.error, ymax = estimate + 2 * std.error)) +
  geom_point() +
  geom_errorbar()

Example 23.7

sleep_fit <- lmer(Reaction ~ Days + (Days | Subject), data = sleepstudy)
summary(sleep_fit)

Linear mixed model fit by REML ['lmerMod']
Formula: Reaction ~ Days + (Days | Subject)
   Data: sleepstudy

REML criterion at convergence: 1743.6

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-3.9536 -0.4634  0.0231  0.4634  5.1793 

Random effects:
 Groups   Name        Variance Std.Dev. Corr
 Subject  (Intercept) 612.10   24.741       
          Days         35.07    5.922   0.07
 Residual             654.94   25.592       
Number of obs: 180, groups:  Subject, 18

Fixed effects:
            Estimate Std. Error t value
(Intercept)  251.405      6.825  36.838
Days          10.467      1.546   6.771

Correlation of Fixed Effects:
     (Intr)
Days -0.138

VarCorr(sleep_fit)

 Groups   Name        Std.Dev. Corr 
 Subject  (Intercept) 24.7407       
          Days         5.9221  0.066
 Residual             25.5918

ranef(sleep_fit)

$Subject
    (Intercept)        Days
308   2.2585509   9.1989758
309 -40.3987381  -8.6196806
310 -38.9604090  -5.4488565
330  23.6906196  -4.8143503
331  22.2603126  -3.0699116
332   9.0395679  -0.2721770
333  16.8405086  -0.2236361
334  -7.2326151   1.0745816
335  -0.3336684 -10.7521652
337  34.8904868   8.6282652
349 -25.2102286   1.1734322
350 -13.0700342   6.6142178
351   4.5778642  -3.0152621
352  20.8636782   3.5360011
369   3.2754656   0.8722149
370 -25.6129993   4.8224850
371   0.8070461  -0.9881562
372  12.3145921   1.2840221

with conditional variances for "Subject"

Example 23.8 (European protected ham) TODO https://cmustatistics.github.io/data-repository/money/european-ham.html

23.4 Random effects as shrinkage

TODO show examples of shrinkage, connect to penalization and bias/variance tradeoff

shrink_pop <- population(
  group = predictor(rfactor, levels = c("A", "B", "C", "D")),
  y = response(
    4 + by_level(group, A = 2, B = 3, C = 1, D = 2.5),
    error_scale = 1
  )
)

shrinks <- shrink_pop |>
  sample_x(n = 100) |>
  sample_y()

shrink_fit <- lm(y ~ group, data = shrinks)
shrink_lmer <- lmer(y ~ (1 | group), data = shrinks)

library(ggplot2)

sampling_distribution(shrink_fit, shrinks, nsim = 1000) |>
  ggplot(aes(x = estimate)) +
  geom_histogram() +
  facet_wrap(vars(term), scales = "free_x")

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.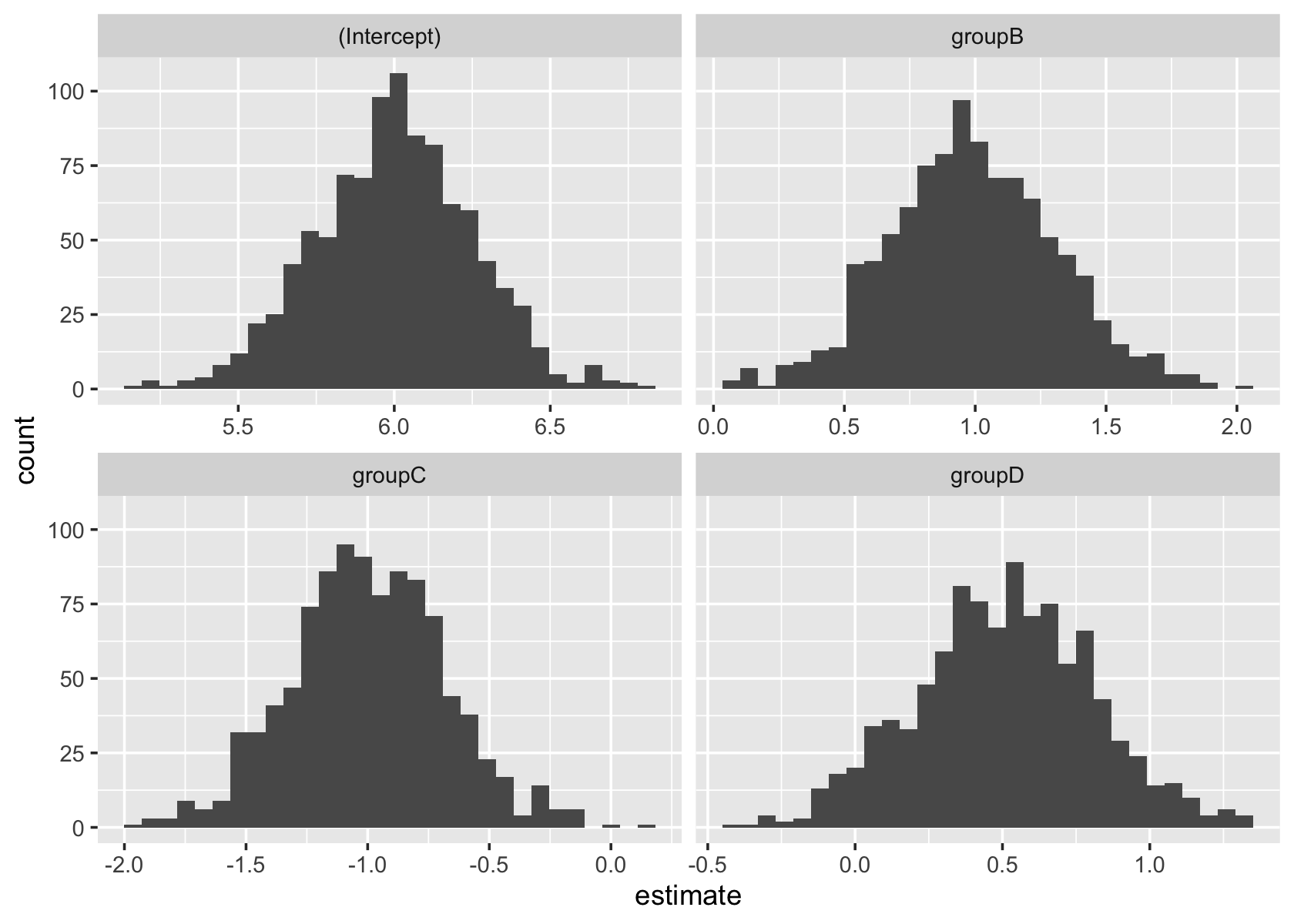

sampling_distribution(shrink_lmer, shrinks, nsim = 1000,
                      function(f) {
                        data.frame(
                          term = rownames(ranef(f)$group),
                          estimate = ranef(f)$group[["(Intercept)"]]
                        )
                      }) |>
  ggplot(aes(x = estimate)) +
  geom_histogram() +
  facet_wrap(vars(term), scales = "free_x")

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.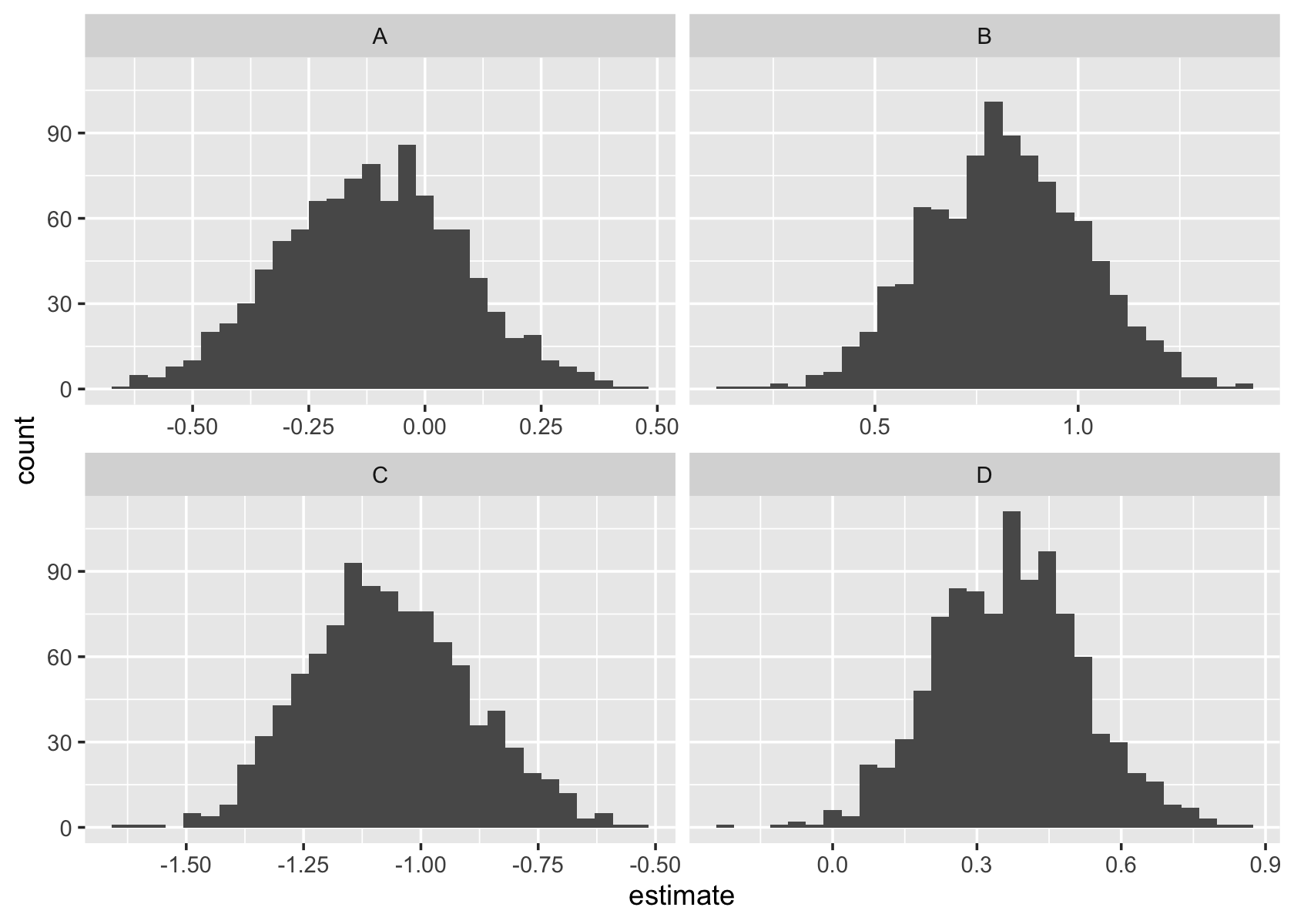

23.5 Exercises

TODO replicate analysis in https://stat.columbia.edu/~gelman/research/unpublished/healing.pdf